Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B , SA vuông góc với ABC ,SA = a√3 . Xác định và tính góc giữa hai mặt phẳng SBC và ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
11 tháng 2 2017
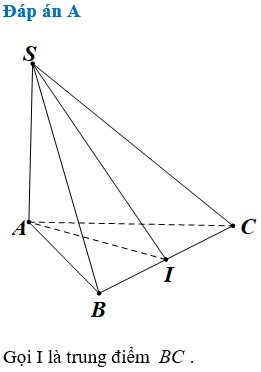
Chọn A.
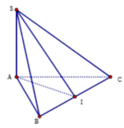
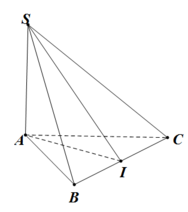
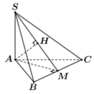
Gọi I là trung điểm của BC, tam giác ABC vuông cân tại A nên AI ⊥ BC
Có SA ⊥ (ABC) => SA ⊥ BC
Suy ra BC ⊥ (SAI). Suy ra ((SBC);(ABC)) = SIA.
∆ SIA vuông tại A có SA = a, AI = a. Suy ra vuông cân tại A.
Suy ra SIA = 45 °

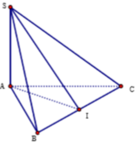

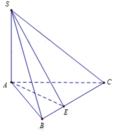


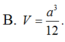

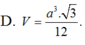


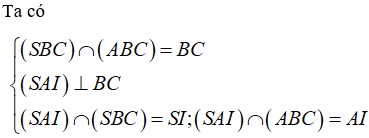
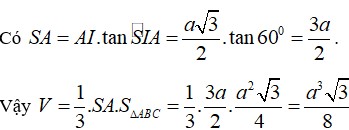
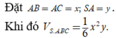
\(SB=\sqrt{\left(a\sqrt{3}\right)^2+a^2}=2a\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{5}\)
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
(SBC;ABC)=(SB;BA)=góc SBA=60 độ