trong mặt phẳng tọa độ Oxy cho đường tròn (c): \(x^2+y^2+2x-6y+5=0.\) gọi \(\Delta\) là tiếp tuyến của (c) tại điểm A(0;1).tìm pt tổng quát của \(\Delta\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(d')//(d)
=>(d'): 4x-3y+c=0
(C): x^2-4x+4+y^2+6y+9-16=0
=>(x-2)^2+(y+3)^2=16
=>R=4; I(2;-3)
Theo đề, ta có: d(I;(d'))=4
=>\(\dfrac{\left|2\cdot4+\left(-3\right)\cdot\left(-3\right)+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=4\)
=>|c+17|=4*5=20
=>c=3 hoặc c=-37

a) Biểu thức tọa độ của hai vt \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \) là \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0}} \right)\), \(\overrightarrow {{M_0}I} = \left( {a - {x_0};b - {y_0}} \right)\)
b) Ta có:
\(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = \left( {x - {x_0}} \right)\left( {a - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right)\)
c) \(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = 0 \Rightarrow \overrightarrow {{M_0}M} \bot \overrightarrow {{M_0}I} \)
Mà \({M_0}I\) là đoạn thẳng nối tâm với điểm nằm ngoài
Vậy ta thấy pt đường thẳng \(M{M_0}\) là tiếp tuyến của đường tròn tại điểm \({M_0}\)

Đường tròn (C) có tâm I (3 ; 3) và có bán kính
\(R = \sqrt {{a^2} + {b^2} - c} = \sqrt {9 + 9 - 14} = 2\)
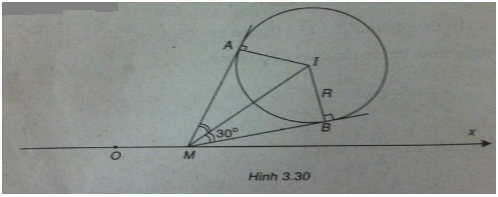
Điểm M(x;0) thuộc Ox.
Từ M kẻ hai tiếp tuyến tiếp xúc với (C) tại A và B. Ta có:
\(\widehat {AMB} = {60^ \circ } \Rightarrow \widehat {IMB} = {30^ \circ }\)
\(\Rightarrow IM = {R \over {\sin {{30}^ \circ }}} = 2R = 4\)
\(IM = 4 \Leftrightarrow \sqrt {{{\left( {x - 3} \right)}^2} + 9} = 4\)
\(\Leftrightarrow {x^2} - 6x + 2 = 0\)
\(\Leftrightarrow x = 3 \pm \sqrt 7\)
Vậy có hai điểm M thỏa mãn đề bài, chúng có tọa độ là :
\({M_1}\left( {3 + \sqrt 7 ;0} \right)\) và \({M_2}\left( {3 - \sqrt 7 ;0} \right)\)

Tọa độ điểm A, B là nghiệm của hệ phương trình :
\(\begin{cases}\left(x+1\right)^2+\left(y-2\right)^2=13\\x-5y-2=0\end{cases}\) \(\Leftrightarrow\begin{cases}26y^2+26y=0\\x=5y+2\end{cases}\)
\(\Leftrightarrow\begin{cases}\begin{cases}x=2\\y=0\end{cases}\\\begin{cases}x=-3\\y=-1\end{cases}\end{cases}\)
\(\Rightarrow A\left(2;0\right);B\left(-3;-1\right)\) hoặc \(A\left(-3;-1\right);B\left(2;0\right)\)
Vì tam giác ABC vuông tại B và nội tiếp đường tròn (C) nên AC là đường kính của đường tròn (C). Hay tâm \(I\left(-1;2\right)\) là trung điểm của AC
Khi đó : \(A\left(2;0\right);B\left(-3;-1\right)\Rightarrow C\left(-4;4\right)\)
\(A\left(-3;-1\right);B\left(2;0\right)\Rightarrow C\left(1;5\right)\)
Vậy \(C\left(-4;4\right)\) hoặc \(C\left(1;5\right)\)

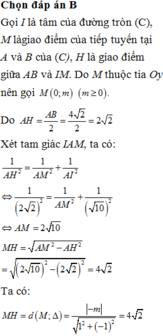

Vì `(C): x^2+y^2+2x-6y+5=0`
`=>I(-1;3)`
Ta có: `\vec{IA}=(1;-2)`
`=>\vec{n_{\Delta}}=(1;-2)`
Mà `A(0;1) in \Delta`
`=>` PTTQ của `\Delta` là: `x-2(y-1)=0<=>x-2y+2=0`