Vì sao giá trị \[\frac{{{{\rm{k}}_{\rm{t}}}}}{{{{\rm{k}}_{\rm{n}}}}}\] là một hằng số ở nhiệt độ xác định?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(5{{\rm{x}}^3} + 8{{\rm{x}}^3} = (5 + 8){x^3} = 13{{\rm{x}}^3}\)
b) \(10y^7 - 15y^7 = (10 - 15)y^7 = -5y^7\)

Hàm số xác định khi: \(\sin x - 1\; \ne 0\; \Leftrightarrow \sin x \ne 1\; \Leftrightarrow x \ne \frac{\pi }{2} + k2\pi ,\;\;k \in \mathbb{Z}\)
Vậy ta chọn đáp án B

a) Vị trí ban đầu ứng với \(t = 0\), suy ra vật thể ở vị trí có tọa độ là \(A\left( {2;5} \right)\).
Vị trí kết thúc ứng với \(t = 180\) , suy ra vật thể ở vị trí có tọa độ là \(B\left( {2;3} \right)\).
b) Từ đẳng thức \({\left( {\sin {t^o}} \right)^2} + {\left( {\cos {t^o}} \right)^2} = 1\) ta suy ra \({\left( {{x_M} - 2} \right)^2} + {\left( {{y_M} - 4} \right)^2} = 1\)
Do đó, M thuộc đường tròn \(\left( C \right)\) có phương trình \({\left( {x - 2} \right)^2} + {\left( {y - 4} \right)^2} = 1\)
Đường tròn có tâm \(I\left( {2;4} \right)\), bán kính \(R = 1\) và nhận AB làm đường kính.
Khi \(t \in \left[ {0;180} \right]\) thì \(\sin t \in \left[ {0;1} \right]\) và \(\cos t \in \left[ { - 1;1} \right]\). Do đó, \(2 + \sin {t^o} \in \left[ {2;3} \right]\) và \(4 + \cos {t^o} \in \left[ {3;5} \right]\).
Vậy quỹ đạo của vật thể là nửa đường tròn đường kính AB vẽ trên nửa mặt phẳng chứa điểm \(C\left( {3;0} \right)\) bờ AB.

\(K_w=10^{-14}\)
\(\Leftrightarrow\left(H^+\right)\left(OH^-\right)=10^{-14}\)
\(\Rightarrow\left(H^+\right)=\dfrac{10^{-14}}{\left(OH^-\right)}=\dfrac{10^{-14}}{2,5.10^{-10}}=4.10^{-5}\left(M\right)\)
\(\Rightarrow pH=-lg\left(4.10^{-5}\right)\approx4,4\)
Vì \(pH< 7\) nên dung dịch trên có môi trường acid.

Ta có: \(\frac{{{\rm{ - a}}{{\rm{x}}^2}{\rm{ - ax}}}}{{{x^2} - 1}} = \frac{{ - a\left( {{x^2} + x} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \frac{{ - ax\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \frac{{{\rm{ - ax}}}}{{x - 1}}\)
Để hai phân thức sau bằng nhau: \(\frac{{{\rm{ - a}}{{\rm{x}}^2}{\rm{ - ax}}}}{{{x^2} - 1}}\) và \(\frac{{3{\rm{x}}}}{{x - 1}}\) khi và chỉ khi a = -3

\(\begin{array}{l}\frac{{2{{\rm{x}}^2} + 1}}{{4{\rm{x}} - 1}} = \frac{{8{{\rm{x}}^3} + 4{\rm{x}}}}{Q}\\ \Rightarrow Q = \frac{{\left( {8{{\rm{x}}^3} + 4{\rm{x}}} \right)\left( {4{\rm{x}} - 1} \right)}}{{2{{\rm{x}}^2} + 1}}\\Q = \frac{{4{\rm{x}}\left( {2{{\rm{x}}^2} + 1} \right)\left( {4{\rm{x}} - 1} \right)}}{{2{{\rm{x}}^2} + 1}}\\Q = 4{\rm{x}}\left( {4{\rm{x}} - 1} \right) = 16{{\rm{x}}^2} - 4{\rm{x}}\end{array}\)
Đáp án D
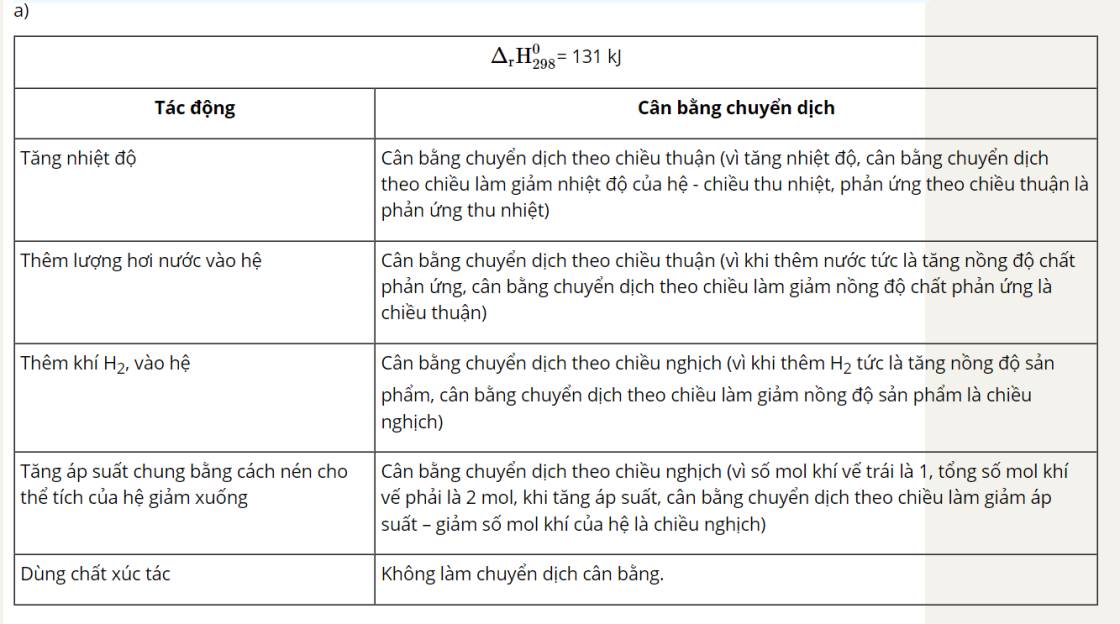
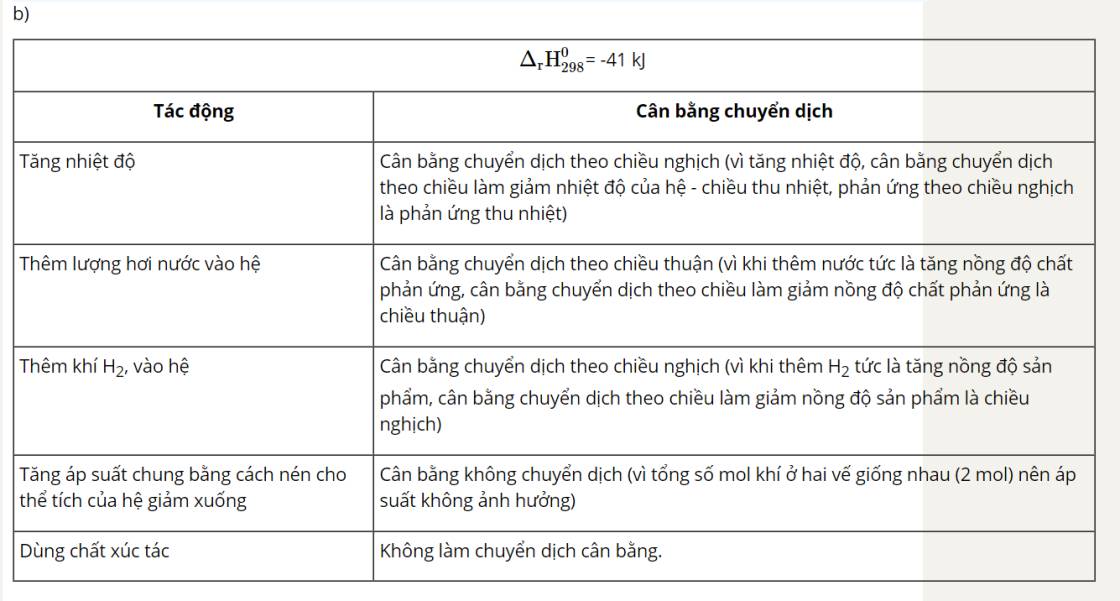
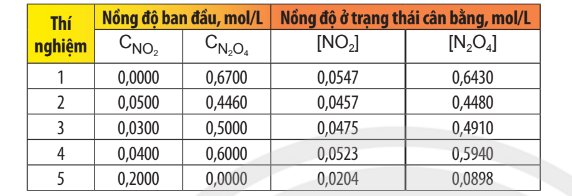
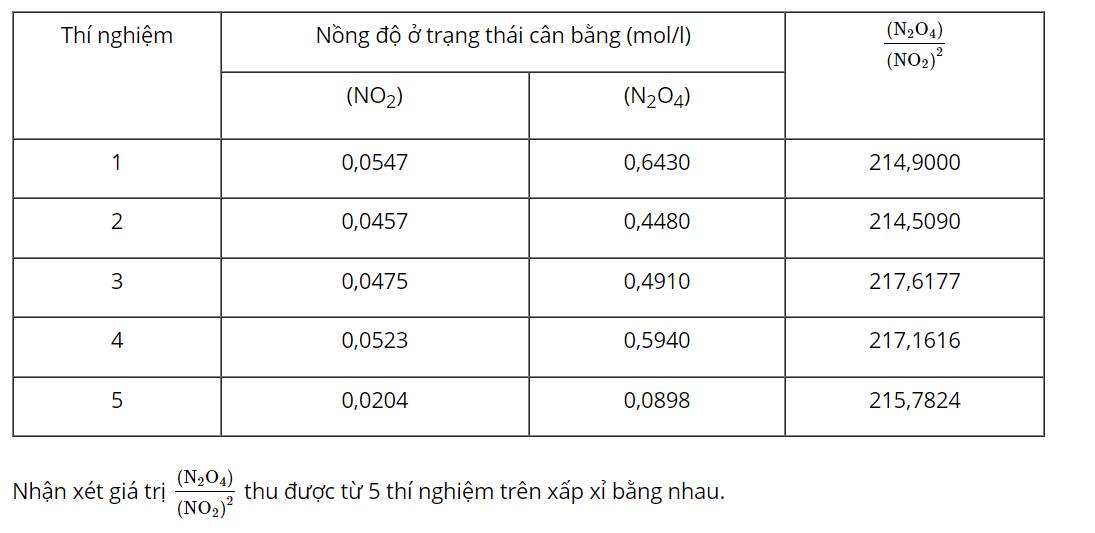
H2(g) + I2(g) ⇌ 2HI
\[\begin{array}{l}{{\rm{v}}_{\rm{t}}}{\rm{ = }}{{\rm{k}}_{\rm{t}}}{{\rm{C}}_{{{\rm{H}}_{\rm{2}}}}}{{\rm{C}}_{{{\rm{I}}_{\rm{2}}}}}\\{{\rm{v}}_{\rm{n}}}{\rm{ = }}{{\rm{k}}_{\rm{n}}}{\rm{C}}_{{\rm{HI}}}^{\rm{2}}\end{array}\]
Với kt và kn lần lượt là hằng số tốc độ phản ứng thuận và hằng số tốc độ phản ứng nghịch.
kt và kn chỉ phụ thuộc vào nhiệt độ nên giá trị \[\frac{{{{\rm{k}}_{\rm{t}}}}}{{{{\rm{k}}_{\rm{n}}}}}\] là một hằng số ở nhiệt độ xác định.