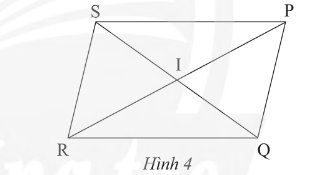
Cho hình bình hành \(PQRS\) với \(I\) là giao điểm của hai đường chéo (Hình 4). Hãy chỉ ra các đoạn thẳng bằng nhau và các góc bằng nhau có trong hình.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

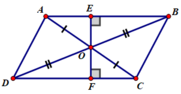
- Hình bình hành ABCD có O là giao điểm của hai đường chéo ⇒ O là trung điểm mỗi đường nên A và C đối xứng nhau qua tâm O
B và D đối xứng nhau qua tâm O
- Xét hai tam giác vuông AEO và CFO có:
OA = OC (do O là trung điểm AC)
∠(AOE) = ∠(COF)(hai góc đối đỉnh)
⇒ ΔAEO = ΔCFO (cạnh huyền – góc nhọn kề)
⇒ OE = OF (hai cạnh tương ứng)
Nên O là trung điểm EF
⇒ E và F đối xứng nhau qua tâm O

Đáp án: B
a sai vì trực tâm là giao điểm của ba đường cao, không phải ba đường phân giác.
b sai vì hai đường chéo của hình bình hành không bằng nhau.
c, d, e đúng.

Hai góc C và D bằng nhau
⇒ Hình thang có hai đường chéo bằng nhau là hình thang cân

a) Hình bình hành, hình chữ nhật, hình thoi, hình vuông
b) Hình chữ nhật, hình vuông
c) Hình bình hành, hình chữ nhật, hình thoi, hình vuông
d) Hình thoi, hình vuông
e) Hình thoi, hình vuông
Các đoạn thẳng bằng nhau là: SP = RQ; SR = PQ; IR = IP; IS = IQ.
Các góc bằng nhau là: \(\widehat{RSQ}=\widehat{SQP},\widehat{PSQ}=\widehat{RQS},\widehat{SIR}=\widehat{PIQ},\widehat{SIP}=\widehat{RIQ}.\)