A=√3x2+6x+12+√5x4−10x2+9=−2x2−4x+3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`@` `\text {Ans}`
`\downarrow`
`a)`
Thu gọn:
`P(x)=`\(5x^4 + 3x^2 - 3x^5 + 2x - x^2 - 4 +2x^5\)
`= (-3x^5 + 2x^5) + 5x^4 + (3x^2 - x^2) + 2x - 4`
`= -x^5 + 5x^4 + 2x^2 + 2x - 4`
`Q(x) =`\(x^5 - 4x^4 + 7x - 2 + x^2 - x^3 + 3x^4 - 2x^2\)
`= x^5 + (-4x^4 + 3x^4) - x^3 + (x^2 - 2x^2) + 7x - 2`
`= x^5 - x^4 - x^3 - x^2 + 7x - 2`
`@` Tổng:
`P(x)+Q(x)=`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) + (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)
`= -x^5 + 5x^4 + 2x^2 + 2x - 4 + x^5 - x^4 - x^3 - x^2 + 7x - 2`
`= (-x^5 + x^5) - x^3 + (5x^4 - x^4) + (2x^2 - x^2) + (2x + 7x) + (-4-2)`
`= 4x^4 - x^3 + x^2 + 9x - 6`
`@` Hiệu:
`P(x) - Q(x) =`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) - (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)
`= -x^5 + 5x^4 + 2x^2 + 2x - 4 - x^5 + x^4 + x^3 + x^2 - 7x + 2`
`= (-x^5 - x^5) + (5x^4 + x^4) + x^3 + (2x^2 + x^2) + (2x - 7x) + (-4+2)`
`= -2x^5 + 6x^4 + x^3 + 3x^2 - 5x - 2`
`b)`
`@` Thu gọn:
\(H (x) = ( 3x^5 - 2x^3 + 8x + 9) - ( 3x^5 - x^4 + 1 - x^2 + 7x)\)
`= 3x^5 - 2x^3 + 8x + 9 - 3x^5 + x^4 - 1 + x^2 - 7x`
`= (3x^5 - 3x^5) + x^4 - 2x^3 - x^2 + (8x + 7x) + (9+1)`
`= x^4 - 2x^3 - x^2 + 15x + 10`
\(R( x) = x^4 + 7x^3 - 4 - 4x ( x^2 + 1) + 6x\)
`= x^4 + 7x^3 - 4 - 4x^3 - 4x + 6x`
`= x^4 + (7x^3 - 4x^3) + (-4x + 6x) - 4`
`= x^4 + 3x^3 + 2x - 4`
`@` Tổng:
`H(x)+R(x)=` \((x^4 - 2x^3 - x^2 + 15x + 10)+(x^4 + 3x^3 + 2x - 4)\)
`= x^4 - 2x^3 - x^2 + 15x + 10+x^4 + 3x^3 + 2x - 4`
`= (x^4 + x^4) + (-2x^3 + 3x^3) - x^2 + (15x + 2x) + (10-4)`
`= 2x^4 + x^3 - x^2 + 17x + 6`
`@` Hiệu:
`H(x) - R(x) =`\((x^4 - 2x^3 - x^2 + 15x + 10)-(x^4 + 3x^3 + 2x - 4)\)
`=x^4 - 2x^3 - x^2 + 15x + 10-x^4 - 3x^3 - 2x + 4`
`= (x^4 - x^4) + (-2x^3 - 3x^3) - x^2 + (15x - 2x) + (10+4)`
`= -5x^3 - x^2 + 13x + 14`
`@` `\text {# Kaizuu lv u.}`

a) 9 x 4 − 10 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 9 t 2 − 10 t + 1 = 0 ( 2 )
Giải (2):
Có a = 9 ; b = -10 ; c = 1
⇒ a + b + c = 0
⇒ Phương trình (2) có nghiệm t 1 = 1 ; t 2 = c / a = 1 / 9
Cả hai nghiệm đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1.
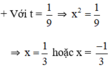
Vậy phương trình (1) có tập nghiệm 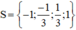
b)
5 x 4 + 2 x 2 - 16 = 10 - x 2 ⇔ 5 x 4 + 2 x 2 - 16 - 10 + x 2 = 0 ⇔ 5 x 4 + 3 x 2 - 26 = 0
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 5 t 2 + 3 t − 26 = 0 ( 2 )
Giải (2) :
Có a = 5 ; b = 3 ; c = -26
⇒ Δ = 3 2 − 4.5 ⋅ ( − 26 ) = 529 > 0
⇒ Phương trình có hai nghiệm phân biệt
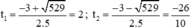
Đối chiếu điều kiện chỉ có t 1 = 2 thỏa mãn
+ Với t = 2 ⇒ ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2.
Vậy phương trình (1) có tập nghiệm S = {-√2; √2}
c) 0 , 3 x 4 + 1 , 8 x 2 + 1 , 5 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó, (1) trở thành : 0 , 3 t 2 + 1 , 8 t + 1 , 5 = 0 ( 2 )
Giải (2) :
có a = 0,3 ; b = 1,8 ; c = 1,5
⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm t 1 = − 1 và t 2 = − c / a = − 5
Cả hai nghiệm đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
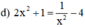
Điều kiện xác định: x ≠ 0.
Quy đồng, khử mẫu ta được :
2 x 4 + x 2 = 1 − 4 x 2 ⇔ 2 x 4 + x 2 + 4 x 2 − 1 = 0 ⇔ 2 x 4 + 5 x 2 − 1 = 0 ( 1 )
Đặt t = x 2 , điều kiện t > 0.
Khi đó (1) trở thành : 2 t 2 + 5 t - 1 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 5 ; c = -1
⇒ Δ = 5 2 − 4.2 ⋅ ( − 1 ) = 33 > 0
⇒ Phương trình có hai nghiệm phân biệt:
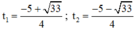
Đối chiếu với điều kiện thấy có nghiệm t 1 thỏa mãn.
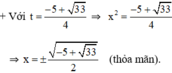
Vậy phương trình có tập nghiệm 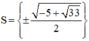

b: \(\dfrac{\left(x^2-1\right)\left(x^2+1\right)-2x\left(x^2-1\right)}{x^2-1}\)
\(=x^2-2x+1\)
\(=\left(x-1\right)^2\)
c: \(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)
\(=5x^3+14x^2+12x+8\)

a: Ta có: \(A=x^2-2xy+5y^2+4y+51\)
\(=x^2-2xy+y^2+4y^2+4y+1+50\)
\(=\left(x-y\right)^2+\left(2y+1\right)^2+50\ge50\forall x,y\)
Dấu '=' xảy ra khi \(x=y=-\dfrac{1}{2}\)
a) \(A=x^2-2xy+5y^2+4y+51=\left(x^2-2xy+y^2\right)+\left(4y^2+4y+1\right)+50=\left(x-y\right)^2+\left(2y+1\right)^2+50\ge50\)
\(minA=50\Leftrightarrow x=y=-\dfrac{1}{2}\)
c) \(C=\dfrac{9}{-2x^2+4x-7}=\dfrac{9}{-2\left(x^2-2x+1\right)-5}=\dfrac{9}{-2\left(x-1\right)^2-5}\ge\dfrac{9}{-5}=-\dfrac{9}{5}\)
\(minC=-\dfrac{9}{5}\Leftrightarrow x=1\)
d) \(10x^2+4y^2-4xy+8x-4y+20=\left[4y^2-4y\left(x+1\right)+\left(x+1\right)^2\right]+\left(9x^2+6x+1\right)+18=\left(2y-x-1\right)^2+\left(3x+1\right)^2+18\ge18\)
\(minD=18\Leftrightarrow\) \(\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)
e) \(E=9x^2+2y^2+6xy-6x-8y+10=\left[9x^2+6x\left(y-1\right)+\left(y-1\right)^2\right]+\left(y^2-6x+9\right)=\left(3x+y-1\right)^2+\left(y-3\right)^2\ge0\)
\(minE=0\Leftrightarrow\) \(\left\{{}\begin{matrix}x=-\dfrac{2}{3}\\y=3\end{matrix}\right.\)

a) P(x)=4x2-6x+a; Q(x)=x-3
Lấy P(x):Q(x)=4x-6 dư a+30
Vậy để P(x)⋮Q(x) ⇒ a+30=0 ⇒ a=-30
b) P(x)=2x2+x+a; Q(x)=x+3
Lấy P(x):Q(x)=2x-7 dư a+21
Vậy để P(x)⋮Q(x) ⇒ a+21=0 ⇒ a=-21
c) P(x)=x3+ax2-4; Q(x)=x2+4x+4
Lấy P(x):Q(x)=x+a-4 dư -4(a-5)x+12
Vậy để P(x)⋮Q(x) ⇒ -4(a-5)x+12=0 ⇒ (a-5)x=3
⇒ a-5 ϵ {-1;1;-3;3} (a ϵ Z)
⇒ a ϵ {4;6;2;8}
d) P(x)=2x2+ax+1; Q(x)=x-3
Lấy P(x):Q(x)=2x+a+6 dư 3a+19
Vậy để P(x)⋮Q(x) ⇒ 3a+19=0 ⇒ a=-19/3
e) P(x)=ax5+5x4-9; Q(x)=x-1
Lấy P(x):Q(x)=ax4+(a-5)x3+(a-5)x2+(a-5)x+1 dư a-4
Vậy để P(x)⋮Q(x) ⇒ a-4=0 ⇒ a=4
f) P(x)=6x3-x2-23x+a; Q(x)=2x+3
Lấy P(x):Q(x)=3x2-5x-4 dư a+12
Vậy để P(x)⋮Q(x) ⇒ a+12=0 ⇒ a=-12
g) P(x)=x3-6x2+ax-6 Q(x)=x-2
Lấy P(x):Q(x)=x2-2x+a-4 dư 2(a-4)-6
Vậy để P(x)⋮Q(x) ⇒ 2(a-4)-6=0 ⇒ a=7
Bài h có a,b bạn xem lại đề

Bài yêu cầu rút gọn và sắp xếp lại phải không bạn?
\(A\left(x\right)=3x^4+10x^2+9\)
\(B\left(x\right)=x^4-5x^2-8\)