Gọi n là số quả cầu lấy ra. \(\left(n\in N^{\text{*}};1\le n\le9\right)\)

Không gian mẫu \(\left|\Omega\right|=C^n_9\)

Biến cố A : " Có ít nhất 1 số chia hết cho 4"

=> Biến cố \(\overline{A}\) : " Không có số nào chia hết cho 4"

\(\Rightarrow\left|\Omega_{\overline{A}}\right|=C^n_7\\ \Rightarrow P_{\overline{A}}=\dfrac{C^n_7}{C^n_9}=\dfrac{\left(9-n\right)\left(8-n\right)}{8\cdot9}=1-P_A< \dfrac{1}{6}\\ \Rightarrow n^2-17n+72< 12\\ \Rightarrow5< n< 12\)

Vậy cần phải lấy ít nhất 6 quả để XS có ít nhất 1 số chia hết cho 4 > 5/6

Chọn đáp án C

Cách 1: Gọi P n A  là xác suất rút ít nhất được một thẻ ghi số chia hết cho 4 từ n lần rút.

Gọi  P n B  là xác suất không rút được thẻ ghi số chia hết cho 4 từ n lần rút.

cau kho vay ban

Có: `\Omega =C_24 ^5`

Gọi `A:` "Lấy được `5` quả cầu trong đó có ít nhất `1` quả cầu đỏ."

  `=>\overline{A}=C_17 ^5`

`=>P(A)=1-[C_17 ^5]/[C_24 ^5]=1297/1518`

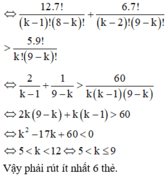
Chia 16 số ra làm 3 tập:
A={1;4;7;10;13;16}; B={2;5;8;11;14}; C={3;6;9;12;15}

TH1: 1 số trong A, 1 số trong B, 1 số trong C

=>Có 6*5*5=150 cách

TH2: 3 số trong A

=>Có \(C^3_6=20\left(cách\right)\)

TH3: 3 số trong B hoặc C

=>Có \(C^3_5\cdot2=20\left(cách\right)\)

=>n(A)=20+20+150=190

\(n\left(omega\right)=C^3_{16}=560\)

=>P(A)=19/56

\(n\left(\Omega\right)=C^3_{30}=4060\)

n(A)\(C^1_{15}\cdot C^2_{15}=1575\)

=>P=1575/4060=45/116

Xác suất lấy ra quả cầu không có số 1 hoặc số 5 từ túi đầu tiên: \(\frac{8}{{10}} = \frac{4}{5}\)

Xác suất lấy được quả cầu không có số 1 hoặc số 5 từ túi thứ hai là: \(\frac{8}{{10}} = \frac{4}{5}\)

Vì lấy ngẫu nhiên từ hai túi khác nhau một quả cầu nên hai biến cố quả cầu lấy ra mỗi túi không có số 1 hoặc số 5 là độc lập.

Vậy xác suất để trong hai quả cầu được lấy ra không có quả cầu nào ghi số 1 hoặc ghi số 5 là: \(\frac{4}{5}.\frac{4}{5} = \frac{{16}}{{25}}\)

-         Số cách lấy ngẫu nhiên 2 quả cầu: \(n\left( \Omega  \right) = C_9^2 = 36\)

-         Số cách lấy 2 quả khác màu là:

+ 1 quả màu xanh và 1 quả màu vàng: \(C_4^1 \times C_3^1 = 12\)

+ 1 quả màu xanh và 1 quả màu đỏ: \(C_4^1 \times C_2^1 = 8\)

+ 1 quả màu đỏ và 1 quả màu vàng: \(C_2^1 \times C_3^1 = 6\)

=> Tổng số cách lấy ra 2 quả khác màu là: 26 cách

-         Số cách lấy 2 quả khác màu trùng số:

+ 2 quả cùng là số 1: \(C_3^2 = 3\)

+ 2 quả cùng là số 2: \(C_3^2 = 3\)

+ 2 quả cùng là số 3: \(C_2^2 = 1\)

=> Tổng số cách lấy ra 2 quả khác màu trùng số là: 7 cách

=> Số cách lấy ra 2 quả khác màu khác số là: 26 – 7 = 19 (cách)

=> Xác suất để lấy ra 2 quả khác màu khác số là: \(P = \frac{{19}}{{36}}\)