Cho hình chóp S.ABC có SA ⊥ (ABC). Mặt phẳng (P) khác với mặt phẳng (ABC), vuông góc với đường thẳng SA và lần lượt cắt các đường thẳng SB, SC tại hai điểm phân biệt B', C'. Chứng minh rằng B'C' // BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án D
Ta có
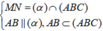
![]()
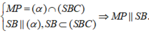
![]()
Khi đó ![]()
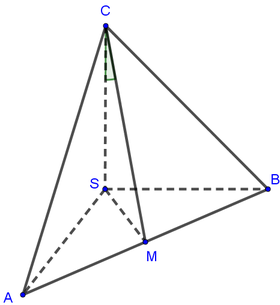
Gọi I là trung điểm của AB.
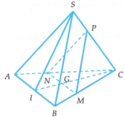
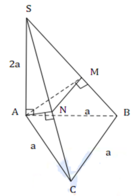
Ta có SA=SB=AB=CA=CB=a nên tam giác SAB và tam giác ABC đều cạnh a.
Khi đó A B ⊥ S I , A B ⊥ C I và S I = C I = a 3 a
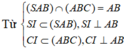
![]()
Mặt khác S I = C I = S C = a 3 2 nên ∆ S I C đều
![]()
Vậy góc giữa hai mặt phẳng (MNP) và (ABC) bằng 60 0

\(\begin{array}{l}\left. \begin{array}{l}A \in \left( {ABC} \right)\\B \in \left( {ABC} \right)\end{array} \right\} \Rightarrow AB \subset \left( {ABC} \right)\\\left. \begin{array}{l}B \in \left( {ABC} \right)\\C \in \left( {ABC} \right)\end{array} \right\} \Rightarrow BC \subset \left( {ABC} \right)\\\left. \begin{array}{l}A \in \left( {ABC} \right)\\C \in \left( {ABC} \right)\end{array} \right\} \Rightarrow AC \subset \left( {ABC} \right)\end{array}\)
\(SA \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow SA\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(SB \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow SB\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(SC \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow SC\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(A'B \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow A'B\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(A'C \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow A'C\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(B'A \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow B'A\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(B'C \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow B'C\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(C'A \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow C'A\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(C'B \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow C'B\) cắt mặt phẳng \(\left( {ABC} \right)\).
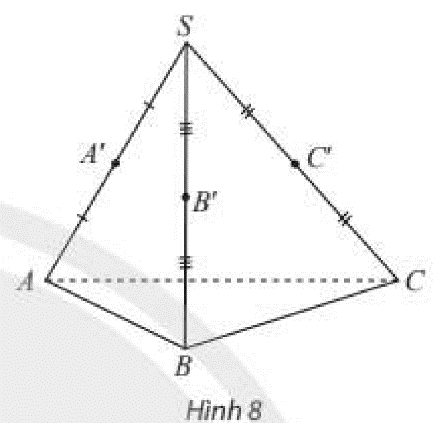
\(A'\) là trung điểm của \(SA\)
\(B'\) là trung điểm của \(SB\)
\( \Rightarrow A'B'\) là đường trung bình của tam giác \(SAB\)
\(\left. \begin{array}{l} \Rightarrow A'B'\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'B'\parallel \left( {ABC} \right)\)
\(A'\) là trung điểm của \(SA\)
\(C'\) là trung điểm của \(SC\)
\( \Rightarrow A'C'\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow A'C'\parallel AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'C'\parallel \left( {ABC} \right)\)
\(B'\) là trung điểm của \(SB\)
\(C'\) là trung điểm của \(SC\)
\( \Rightarrow B'C'\) là đường trung bình của tam giác \(SBC\)
\(\left. \begin{array}{l} \Rightarrow B'C'\parallel BC\\BC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow B'C'\parallel \left( {ABC} \right)\)

Chọn đáp án A
Phương pháp
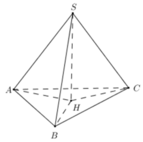
+) Gọi H là hình chiếu của S trên (ABC). Xác định các góc giữa các cạnh bên và đáy.
+) Chứng minh các tam giác SAH, SBH, SCH bằng nhau



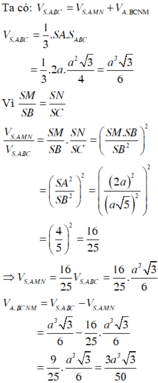
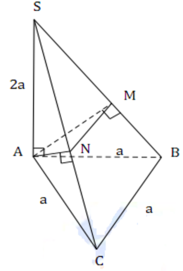
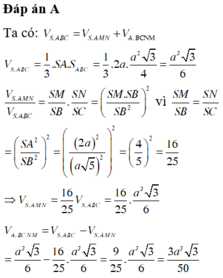
SA vuông góc (P)
SA vuông góc (ABC)
=>(P)//(ABC)
=>B'C'//BC