Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

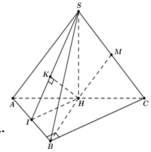
Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.

Phương pháp:
Sử dụng tỉ số diện tích, tỉ số thể tích để tính thể tích khối tứ diện MBSI thông qua thể tích khối tứ diện vuông SABC.
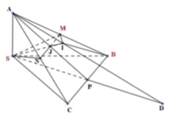

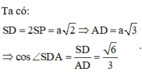
Áp dụng định lí Menelaus trong tam giác APD ta có:

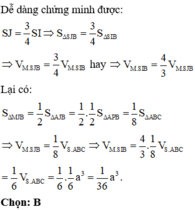

Đáp án D
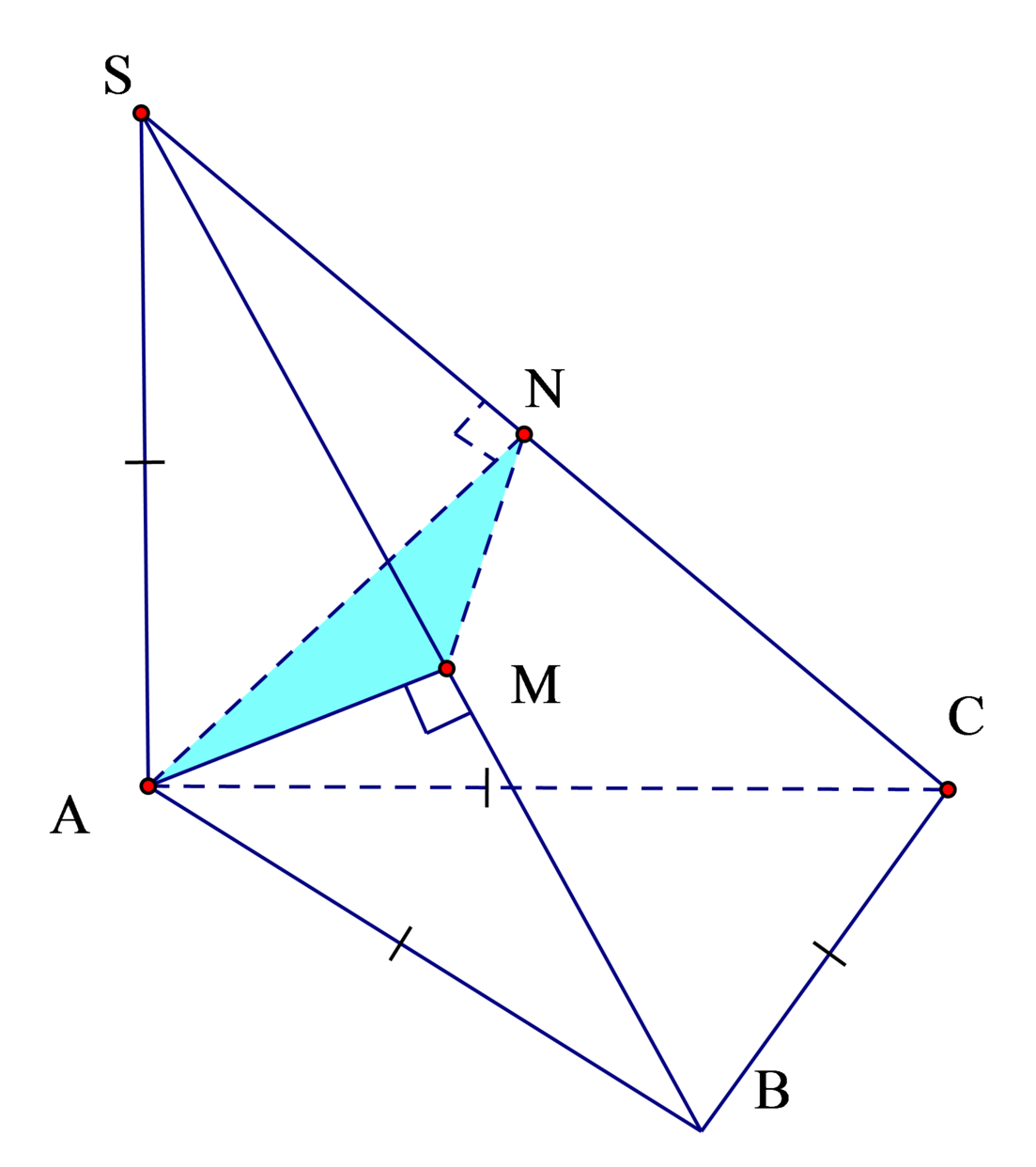
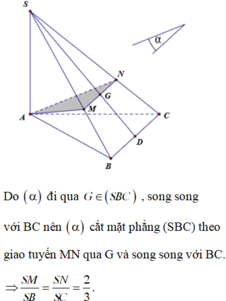
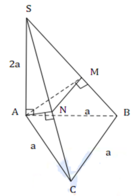
Do Δ S A B , Δ S A C cân nên M, N là trung điểm SB, SC
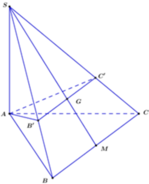
Ta có: V S . A M N V S . A B C = S M S B S N S C = 1 2 1 2 = 1 4 ⇒ V A . B C M N V S . A B C = 3 4
⇒ V A . B C M N = 3 4 V S . A B C = 1 4 S A . d t A B C = 1 4 a . a 2 3 4 = a 3 3 16

Xác định được 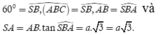
Do M là trung điểm của cạnh AB nên ![]()
![]()
Tam giác vuông SAM, có 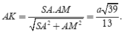
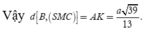
Chọn B.

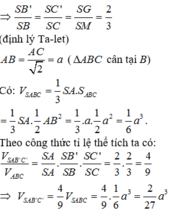

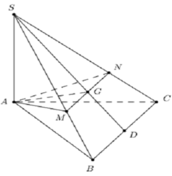

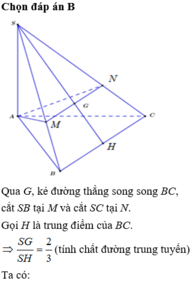

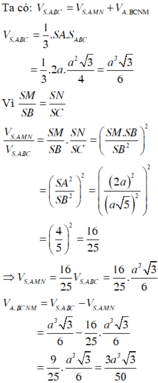
Chọn đáp án D
Ta có
Khi đó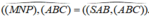
Gọi I là trung điểm của AB.
Ta có SA=SB=AB=CA=CB=a nên tam giác SAB và tam giác ABC đều cạnh a.
Khi đó A B ⊥ S I , A B ⊥ C I và S I = C I = a 3 a
Mặt khác S I = C I = S C = a 3 2 nên ∆ S I C đều
Vậy góc giữa hai mặt phẳng (MNP) và (ABC) bằng 60 0