Người ta xây dựng một cây cầu vượt giao thông hình parabol nối hai điểm có khoảng cách là 400 m (H.9.4). Độ dốc của mặt cầu không vượt quá 100 (độ dốc tại một điểm được xác định bởi góc giữa phương tiếp xúc với mặt cầu và phương ngang như Hình 9.5). Tính chiều cao giới hạn từ đỉnh cầu đến mặt đường (làm tròn kết quả đến chữ số thập phân thứ nhất).


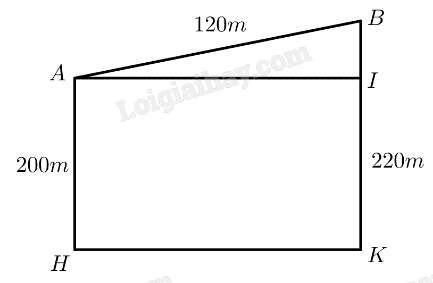


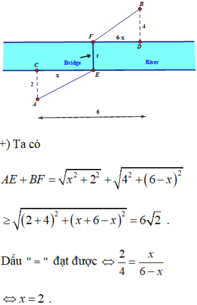
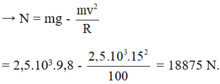
Chọn hệ trục tọa độ Oxy sao cho O là trung điểm AB, tia Ox trùng với tia OB, tia Oy hướng lên trên.
Khi đó \(A\left(-200;0\right),B\left(200;0\right)\). Gọi chiều cao giới hạn của cầu là h (h > 0), suy ra đỉnh cầu có tọa độ (0;h)
Ta tìm được phương trình parabol của cầu là: \(y=-\dfrac{h}{200^2}\cdot x^2+h\)
Ta có: \(y'=-\dfrac{2h}{200^2}\cdot x\), suy ra hệ số góc xác định độ dốc của mặt cầu là
\(k=y'=-\dfrac{2h}{200^2}\cdot x;-200\le x\le200\)
Vì độ dốc của mặt cầu không quá 10o nên ta có: \(\dfrac{h}{100}\le tan10^o\Leftrightarrow h\le17,6\)
Vậy chiều cao giới hạn từ đỉnh cầu tới mặt đường là 17,6cm