cosα = OH¯; sinα = OK¯

Do tam giác OMK vuông tại K nên:

sin2 α + cos2 α = OK¯2 + OH¯2 = OK2 + MK2 = OM2 = 1.

Vậy sin2 α + cos2 α = 1.

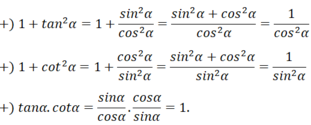
CM HĐT là 

VD CM 

( x + y)^2 = x^2 + 2xy + y^2 

Phải không bạn 

\(\left(x+a\right)\left(x+b\right)\)

=>\(x^2+bx+ax+ab\)

=>\(x^2+\left(a+b\right)x+ab\)(ĐPCM)

Nhớ H cho mik nhé, các bạn.

Biến đổi vế trái:

a + b + c 3 = a + + c 3  = a + b 3 +3 a + b 2  c+3(a+b) c 2 + c 3

      =  a 3  + 3 a 2 b + 3a b 2  +  b 3  + 3( a 2 + 2ab +  b 2 )c + 3a c 2  + 3b c 2  +  c 3

      =  a 3  + 3 a 2 b + 3a b 2  +  b 3  + 3 a 2 c + 6abc + 3 b 2 c + 3a c 2  + 3b c 2 + c3

      =  a 3 +  b 3  +  c 3  + 3 a 2 b + 3a b 2 + 3 a 2 c + 6abc + 3 b 2 c + 3a c 2  + 3b c 2

      =  a 3  +  b 3  +  c 3  + (3 a 2 b + 3a b 2 ) +( 3 a 2 c + 3abc)+ (3abc + 3 b 2 c)+(3a c 2  + 3b c 2 )

      =  a 3  +  b 3  +  c 3  + 3ab(a + b) + 3ac(a + b) + 3bc(a + b) + 3 c 2 (a + b)

      =  a 3  +  b 3  +  c 3 + 3(a + b)(ab + ac + bc +  c 2 )

      =  a 3  +  b 3  +  c 3  + 3(a + b)[a(b + c) + c(b + c)]

      =  a 3  +  b 3  +  c 3  + 3(a + b)(b + c)(a + c) (đpcm)

\(x^2+x+\frac{1}{2}\)

\(=x^2+2.x.\frac{1}{2}+\frac{1}{4}-\frac{1}{4}+\frac{1}{2}\)

\(=\left(x+\frac{1}{2}\right)^2+\frac{1}{4}\ge\frac{1}{4}>;0\forall x\)

Vậy đa thức trên vô nghiệm

vế tra= -ab+ac-bc+ab=ac-bc=-c(b-c)

Các bạn giúp mình nha :))

\(a^2+b^2\) = (a+b)\(^2\) - 2ab

ta có

(a+b)\(^2\) - 2ab

= a\(^2\) + 2ab + b\(^2\) - 2ab

= a\(^2\) + b\(^2\) ( đpcm)

Đặt \(A=x-x^2-1\)\(\Rightarrow2A=2x-2x^2-2=-\left(x^2-2x+1\right)-x^2-1=-\left[\left(x-1\right)^2+x^2\right]-1< 0\)

\(\Rightarrow2A< 0\Rightarrow A< 0\)

`K(-1/2)>1?`

`x^2-x>=0?`