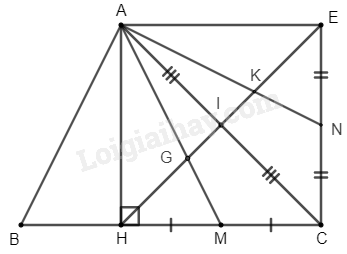
Bài 1: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm AC, E là điểm đối xứng với H qua I. Gọi M,N là trung điểm HC,CE các đường thẳng AM,AN cắt HE tại G và K.
a) Chứng minh: Tứ giác AHCE là hình chữ nhật
b) Chứng minh: HG=GK=KE
Mình đang càn gấp bài này, các bạn giúp mình nhé. Cảm ơn các bạn.

a/
Ta có
IA=IC (gt)
IH=IE (gt)
=> AHCE là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
\(AH\perp BC\Rightarrow\widehat{AHC}=90^o\)
=> AHCE là hình chữ nhật (hình bình hành có 1 góc vuông là HCN)
b/
Xét tg AHC có
MH=MC (gt)
IA=IC (gt)
=> G là trong tâm của tg AHC \(\Rightarrow HG=2IG\) (1)
\(\Rightarrow HG+IG=IH=3IG\) (2)
Chứng minh tương tự ta có K là trọng tâm của tg ACE
\(\Rightarrow KE=2IK\left(3\right)\Rightarrow KE+IK=IE=3IK\) (4)
Mà IH=IE (gt) (5)
Từ (2) (4) (5) => IG=IK (6)
Từ (1) (3) (6) => HG=KE
Mà IG=IK => IG+IKGK=2IK=KE
=> HG=GK=KE