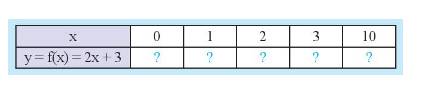
Lượng nước \(y\) (tính theo \({m^3}\)) có trong một bể nước sau \(x\) giờ mở vòi cấp nước được cho bởi hàm số \(y = 2x + 3\). Tính lượng nước có trong bể sau 0 giờ; 1 giờ; 2 giờ; 3 giờ; 10 giờ và hoàn thành bảng giá trị sau:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Lượng nước chảy vào bể sau 1 giờ là:
\(1.2 = 2\left( {{m^3}} \right)\)
b) Lượng nước chảy vào bể sau \(x\) giờ là:
\(2.x = 2x\left( {{m^3}} \right)\)
c) Lượng nước \(y\) có trong bể sau \(x\) giờ là:
\(y = 2x + 5\left( {{m^3}} \right)\).

Sau khi mở vòi nước 2 giò thì lượng nước trong bể bằng: 2/5 x 2 = 4/5 bể
Dùng hết 3/4 lượng nước có trong bể thì còn lại là: 4/5 - 4/5 x 3/4 = 1/5 bể
Lượng nước trong bể sau khi mở vòi trong 2 giờ
\(2\cdot\frac{2}{5}=\frac{4}{5}\) ( bể )
Lượng nước bể còn lại sau khi dùng
\(\frac{4}{5}-\frac{3}{4}=\frac{1}{20}\) ( bể )

trong 1h vòi thứ nhất chảy được số phần bể là: 1:6=1/6bể
trong 1h vòi thứ nhất chảy được số phần bể là: 1:8=1/8 bể
=> trong 1h cả hai vòi chảy được lá : 1/6+1/8=7/24 bể

`Tổng số phần hai vòi chảy trong 1 giờ là `
`3+5=8(phần)`
``Mỗi giờ vòi 1 chảy được là :`
\(\dfrac{4}{5}:8\times3=\dfrac{3}{10}\left(bể\right)\)
`Mỗi giờ vòi 2 chảy được là :`
\(\dfrac{4}{5}:8\times5=\dfrac{1}{2}\left(bể\right)\)

Gọi thời gian vòi 1 chảy một mình đầy bể là x (h)
thời gian vòi 2 chảy một mình đầy bể là y(h)
ĐK : x > 6 ; y > 6
Ta có 1 giờ vòi 1 chảy được \(\dfrac{1}{x}\) (bể)
1 giờ vòi 2 chảy được \(\dfrac{1}{y}\)(bể)
1 giờ 2 vòi chảy được \(\dfrac{1}{6}\left(bể\right)\)
=> PT : \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\)(1)
mà vòi 1 chảy trong 2 giờ rồi khóa ; vòi 2 chảy tiếp 3 giờ được 40% bể
=> PT \(\dfrac{2}{x}+\dfrac{3}{y}=\dfrac{2}{5}\)(2)
Từ (1) (2) => HPT : \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{2}{x}+\dfrac{3}{y}=\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{2}{y}=\dfrac{1}{3}\\\dfrac{2}{x}+\dfrac{3}{y}=\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{1}{y}=\dfrac{1}{15}\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=10\\y=15\end{matrix}\right.\)(tm)
Vậy...
Sau khi tăng chiều dài thêm \(x\left( m \right)\) thì chiều dài mới của hình chữ nhật là \(3 + x\left( m \right)\)
Sau khi tăng chiều rộng thêm \(x\left( m \right)\) thì chiều rộng mới của hình chữ nhật là \(2 + x\left( m \right)\)
Chu vi mới của hình chữ nhật là:
\(y = \left( {3 + x + 2 + x} \right).2\)
\( \Leftrightarrow y = \left( {5 + 2x} \right).2\)
\( \Leftrightarrow y = 4x + 10\)
Vì hàm số \(y = 4x + 10\) có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\).
Nên hàm số \(y = 4x + 10\) là hàm số bậc nhất.
Do đó \(y\) là một hàm số bậc nhất theo biến số \(x\), hệ số \(a = 4;b = 10\).