Cho tam giác ABC vuông tại A có góc B = 30 độ .
a) Tính góc C
b) vẽ tia phân giác của góc C cắt cạnh AB tại D . Trên cạnh CB lấy điểm M sao cho CM = CA . CMR : tam giác ACD = tam giác MCD .
Qua C vẽ đường thẳng xy vuông góc CA . Từ A kẻ đường thẳng // vs CD cắt xy ở K . Cm : AK = CD
c) tính góc AKC

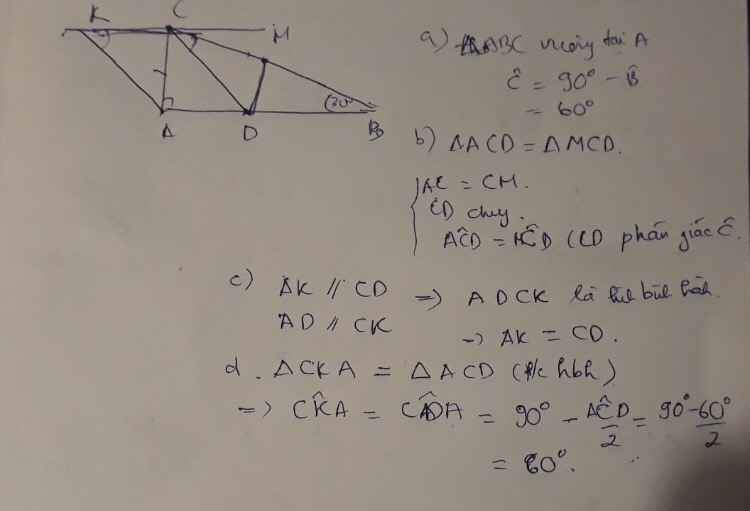
mình vẽ hình rồi, còn phần chứng minh làm như bạn Trần Hoàng Việt nha!!
a) Ta có : A=900 ; B=300
=> C=180-A-B=180-90-30=60
b) Xét tam giác ACD và MCD ta có :
CD chung (1)
CM=CA (gt)(2)
góc ACD=góc DCM (gt) (3)
Từ (1)(2)(3) =>\(\Delta\)ACD=\(\Delta\)MCD (c.g.c)
c) Ta có :AK//CD; CK//AD => tứ giác ADCK là hình bình hành
=>AK=CD (cặp cạnh tương ứng )
d)Ta có : \(\widehat{BDC}\)=180-30-60:2=1200
\(\widehat{CPA}\)=180-120=60
Do ADCK là hình bình hành nên \(\widehat{CPA}\)=\(\widehat{AKC}\)=\(60^0\)