Bài 10: Cho ▲ABC vuông tại A có AB < AC, đường cao AH và trung tuyến AE. Gọi D,F lần lượt là hình chiếu của E rên AB, AC. Olaf giao điểm của AE và DF.
a) CM ADEF là hình chữ nhật
b) CM DF // BC
c) CM BDFE là hình bình hành
d) CM F là trung điểm của AC
e) CM DFEH là hình thang cân
f) Lấy M sao cho F là trung điểm của EM và N sao cho F là trung điểm của BN. CM A,N,M thẳng hàng

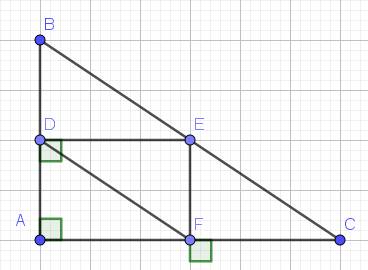
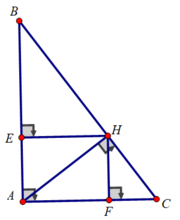
a: Xét tứ giác ADEF có
góc ADE=góc AFE=góc FAD=90 độ
=>ADEF là hình chữ nhật
b: Xét ΔABC có
E là trung điểm của CB
ED//AC
Do đó: D là trung điểm của AB
Xét ΔABC có
E là trung điểm của CB
EF//AB
Do đó: F là trung điểm của AC
Xét ΔABC có
D,F lần lượt là trung điểm của AB,AC
=>DF là đường trung bình
=>DF//BC và DF=1/2BC
c: DF//BC và DF=1/2BC
mà \(E\in BC;BE=\dfrac{1}{2}BC\)
nên DF//BE và DF=BE
Xét tứ giác BDFE có
DF//BE
DF=BE
Do đó: BDFE là hình bình hành
d: Xét ΔABC có
E là trung điểm của CB
EF//AB
Do đó: F là trung điểm của AC
e: Xét ΔABC có
D,E lần lượt là trung điểm của BA,BC
=>DE là đường trung bình
=>DE=1/2AC
ΔHAC vuông tại H
mà HF là trung tuyến
nên HF=AC/2
=>DE=HF
Xét tứ giác DHEF có
DF//EH
DE=FH
Do đó: DHEF là hình thang cân