Tìm giá trị nhỏ nhất của biểu thức P= \(2x^2+\dfrac{7}{2x^2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{2x^2-2x+3}{x^2-x+2}=\dfrac{2\left(x^2-x+2\right)-1}{x^2-x+2}=2-\dfrac{1}{x^2-x+2}=2-\dfrac{1}{x^2-2.\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{7}{4}}=2-\dfrac{1}{\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}}\ge2-\dfrac{1}{\dfrac{7}{4}}=\dfrac{10}{7}\)-Dấu bằng xảy ra \(\Leftrightarrow x=-\dfrac{1}{2}\)

\(A=\dfrac{2x^2-8x+17}{x^2-2x+1}\left(x\ne1\right)\)
\(\Leftrightarrow A\left(x^2-2x+1\right)=2x^2-8x+17\)
\(\Leftrightarrow Ax^2-2Ax+A=2x^2-8x+17\)
\(\Leftrightarrow x^2\left(A-2\right)-2x\left(A-4\right)+A-17=0\left(1\right)\)
\(A-2=0\Leftrightarrow A=2\Leftrightarrow x=3,75\left(tm\right)\left(2\right)\)
\(A-2\ne0\Leftrightarrow A\ne2\Rightarrow\Delta'\ge0\Leftrightarrow\left(A-4\right)^2-\left(A-17\right)\left(A-2\right)\ge0\Leftrightarrow A\ge\dfrac{18}{11}\Rightarrow A_{min}=\dfrac{18}{11}\Leftrightarrow x=\dfrac{13}{2}\left(tm\right)\left(3\right)\)
\(\left(2\right)và\left(3\right)\Rightarrow A_{min}=\dfrac{18}{11}\Leftrightarrow x=\dfrac{13}{2}\)

Đặt \(\sqrt{x^2+4}=a\ge2\)
\(\Rightarrow x^2=a^2-4\)
\(\Rightarrow A=\dfrac{2\left(a^2-4\right)+3}{a+2}=\dfrac{2a^2-5}{a+2}=2a-4+\dfrac{3}{a+2}\)
\(A=\dfrac{3\left(a+2\right)}{16}+\dfrac{3}{a+2}+\dfrac{29}{16}a-\dfrac{35}{8}\ge2\sqrt{\dfrac{9\left(a+2\right)}{16\left(a+2\right)}}+\dfrac{29}{16}.2-\dfrac{35}{8}=\dfrac{3}{4}\)
\(A_{min}=\dfrac{3}{4}\) khi \(a=2\Rightarrow x=0\)

\(P-2015=\dfrac{\left(x-1\right)^2}{x^2}\ge0\) nên \(P\ge2015\), xảy ra dấu bằng khi x = 1.

a: Để \(\dfrac{3x-2}{4}\) không nhỏ hơn \(\dfrac{3x+3}{6}\) thì \(\dfrac{3x-2}{4}>=\dfrac{3x+3}{6}\)
=>\(\dfrac{6\left(3x-2\right)}{24}>=\dfrac{4\left(3x+3\right)}{24}\)
=>18x-12>=12x+12
=>6x>=24
=>x>=4
b: Để \(\left(x+1\right)^2\) nhỏ hơn \(\left(x-1\right)^2\) thì \(\left(x+1\right)^2< \left(x-1\right)^2\)
=>\(x^2+2x+1< x^2-2x+1\)
=>4x<0
=>x<0
c: Để \(\dfrac{2x-3}{35}+\dfrac{x\left(x-2\right)}{7}\) không lớn hơn \(\dfrac{x^2}{7}-\dfrac{2x-3}{5}\) thì
\(\dfrac{2x-3}{35}+\dfrac{x\left(x-2\right)}{7}< =\dfrac{x^2}{7}-\dfrac{2x-3}{5}\)
=>\(\dfrac{2x-3+5x\left(x-2\right)}{35}< =\dfrac{5x^2-7\cdot\left(2x-3\right)}{35}\)
=>\(2x-3+5x^2-10x< =5x^2-14x+21\)
=>-8x-3<=-14x+21
=>6x<=24
=>x<=4
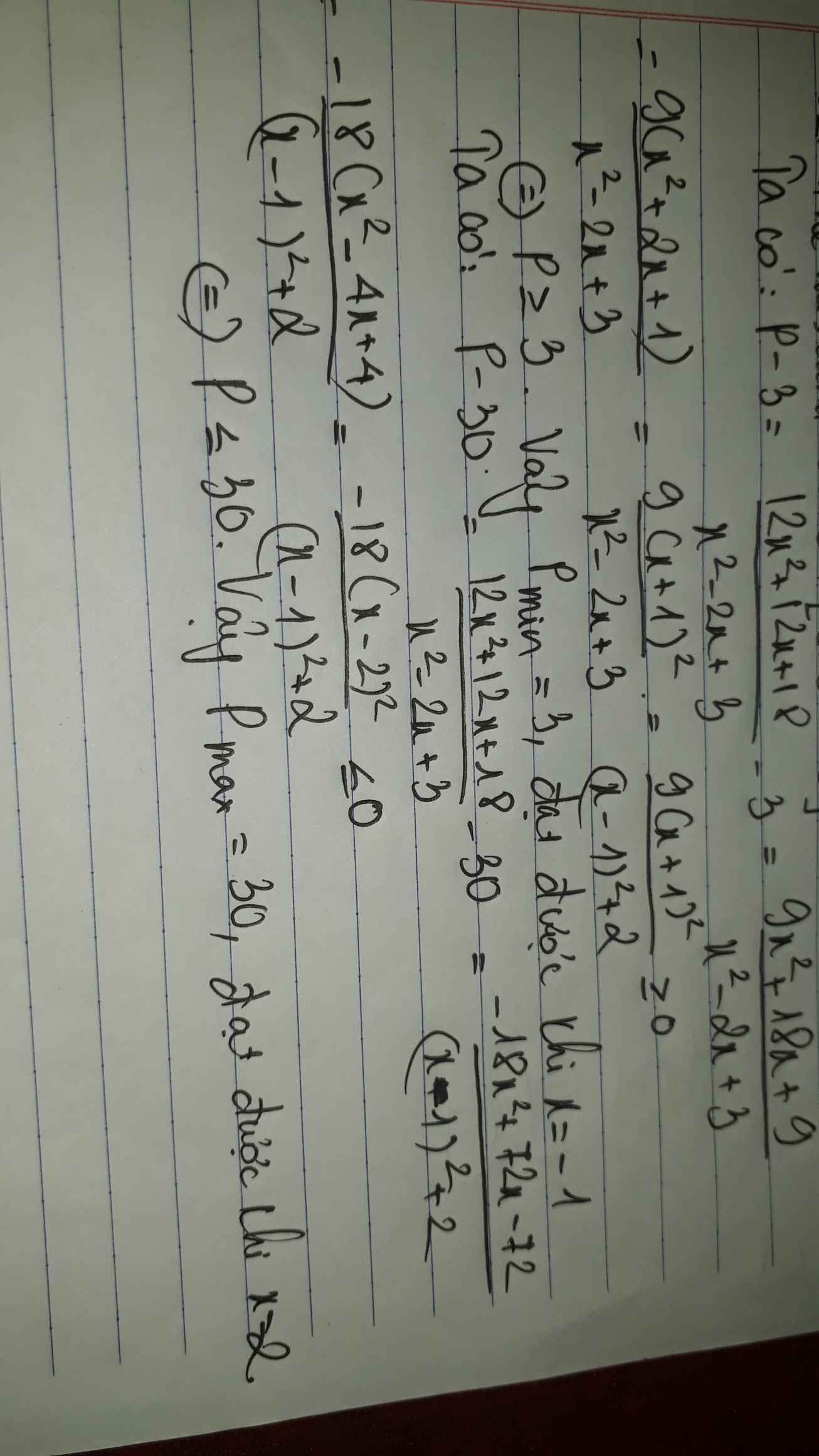
\(P=2x^2+\dfrac{7}{2x^2}\)
Áp dụng Bất đẳng thức Cauchy cho 2 cặp số dương \(\left(2x^2;\dfrac{7}{2x^2}\right)\)
\(P=2x^2+\dfrac{7}{2x^2}\ge2\sqrt[]{7}\)
Dấu "=" xảy ra khi và chỉ khi
\(\Leftrightarrow2x^2=\dfrac{7}{2x^2}\)
\(\Leftrightarrow4x^4=7\left(x\ne0\right)\)
\(\Leftrightarrow x^4=\dfrac{7}{4}\)
\(\Leftrightarrow x=\pm\sqrt[4]{\dfrac{7}{4}}\)
Vậy \(GTNN\left(P\right)=2\sqrt[]{7}\left(tại.x=\pm\sqrt[4]{\dfrac{7}{4}}\right)\)