Trên tia đối của MP lấy điểm D sao cho MP=MD.

Ta có: \(\Delta\)MBP=\(\Delta\)MCD (c.g.c) => BP=CD (2 cạnh tương ứng)

Mà BP=CQ => CD=CQ  => \(\Delta\)DCQ cân tại C => ^CQD= (180⁰-^DCQ)/2

=> ^MPB=^MDC (2 góc tương ứng) ở vị trí so le trong => AB//CD => ^DCQ=^IAK (Đồng vị) 

M là trung điểm PD, N là trung điểm PQ => MN là đường trung bình của \(\Delta\)PDQ

=> MN//DQ hay IK//DQ => ^CQD=^AKI (Đồng vị) 

 => \(\Delta\)AIK có: ^AKI= (180⁰-^IAK)/2 = (180⁰-^DCQ)/2 = ^CQD

=> Tam giác AIK cân tại A (đpcm)

I. Nội qui tham gia "Giúp tôi giải toán"

1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;

2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.

3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.

Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

wefwef

này cái bạn nguyễn xuân toàn kia bị gì thế ? họ là hỏi bài mà !

1.

a. CN và BM cùng vuông góc DE nên CN//BM

\(\Rightarrow\) BMNC là hình thang vuông tại M và N

b. Theo giả thiết BD vuông góc CA \(\Rightarrow\Delta BDC\) vuông tại D

\(\Rightarrow DO\) là trung tuyến ứng với cạnh huyền BC \(\Rightarrow DO=\dfrac{1}{2}BC\)

Tương tự trong tam giác vuông BEC thì EO là trung tuyến ứng với cạnh huyền

\(\Rightarrow EO=\dfrac{1}{2}BC\Rightarrow DO=EO\Rightarrow\) tam giác cân tại O

c. Tam giác DEO cân tại O, mà P là trung điểm DE \(\Rightarrow OP\) là trung tuyến đồng thời là đường cao

\(\Rightarrow OP\perp DE\) \(\Rightarrow OP//CN//BM\)

Mà O là trung điểm BC \(\Rightarrow OP\) là đường trung bình hình thang BMNC

\(\Rightarrow OP=\dfrac{CN+BM}{2}\)

2. Đặt biểu thức là A

Với \(p=2\) ko thỏa mãn

Với \(p=3\Rightarrow A=71\) là SNT

Với \(p>3\) do p là SNT nên p chỉ có 2 dạng \(p=3k+1\) hoặc \(3k+2\)

- Với \(p=3k+1\Rightarrow p^3\) chia 3 dư 1, \(p^2\) chia 3 dư 1, \(11p=9p+2p\) chia 3 dư 2

\(\Rightarrow A\) chia 3 dư 1+1+2+2=6 chia hết cho 3 (ko là SNT) loại

- Với \(p=3k+2\) tương tự, \(p^3\) chia 3 dư 2, \(p^2\) chia 3 dư 1, \(11p\) chia 3 dư 1

\(\Rightarrow\) A chia 3 dư 2+1+1+2=6 vẫn chia hết cho 3 (loại)

Vậy \(p=3\) là giá trị duy nhất thỏa mãn

Em cảm ơn anh nhiều ạ . Anh có thể cho e xin cách làm bài 2 được k ạ

góc MKC=góc MIC=90 độ

=>MCKI nội tiếp

=>góc MIK+góc MCK=180 độ

góc MIB+góc MHB=180 độ

=>MIBH nội tiếp

=>góc MIH=góc MBH

góc MIH+góc MIK

=180 độ-góc MCK+góc MBH

=180 độ

=>H,I,K thẳng hàng

mik ko bt lm bài này bn à . mik thông minh lắm mấy bn mới ngu ấy

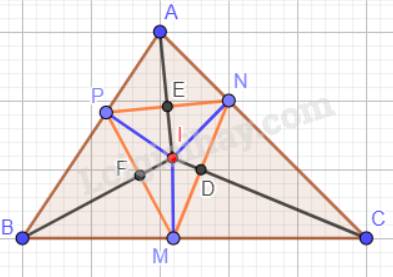
Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM.

Ta có: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.

Xét tam giác vuông INC và tam giác vuông IMC:

     IC chung;

     IN = IM.

Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {MIC} = \widehat {NIC}\)( 2 góc tương ứng).

Tương tự: \(\Delta IPA = \Delta INA\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIA} = \widehat {NIA}\)( 2 góc tương ứng).

     \(\Delta IPB = \Delta IMB\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIB} = \widehat {MIB}\)( 2 góc tương ứng).

Xét hai tam giác IDN và IDM có:

     ID chung;

     \(\widehat {NID} = \widehat {MID}\);

     IN = IM.

Vậy \(\Delta IDN = \Delta IDM\)(c.g.c)

\(\Rightarrow DN = DM\) ( 2 cạnh tương ứng);

 \(\widehat {IDN} = \widehat {IDM}\) ( 2 góc tương ứng)

Mà  \(\widehat {IDN} + \widehat {IDM}=180^0\) ( 2 góc kề bù)

\(\Rightarrow \widehat {IDN} = \widehat {IDM}= 180^0:2=90^0\).

Suy ra: IC là đường trung trực của cạnh MN.

Tương tự ta có:

IA là đường trung trực của cạnh PN; IB là đường trung trực của cạnh PM.

a: góc BPM+góc BRM=180 độ

=>BPMR nội tiếp

b: góc MPC=góc MQC=90 độ

=>MPQC nội tiếp

góc RPM+góc QPM

=góc RBM+góc 180 độ-góc QCM=180 độ

=>R,Q,P thẳng hàng