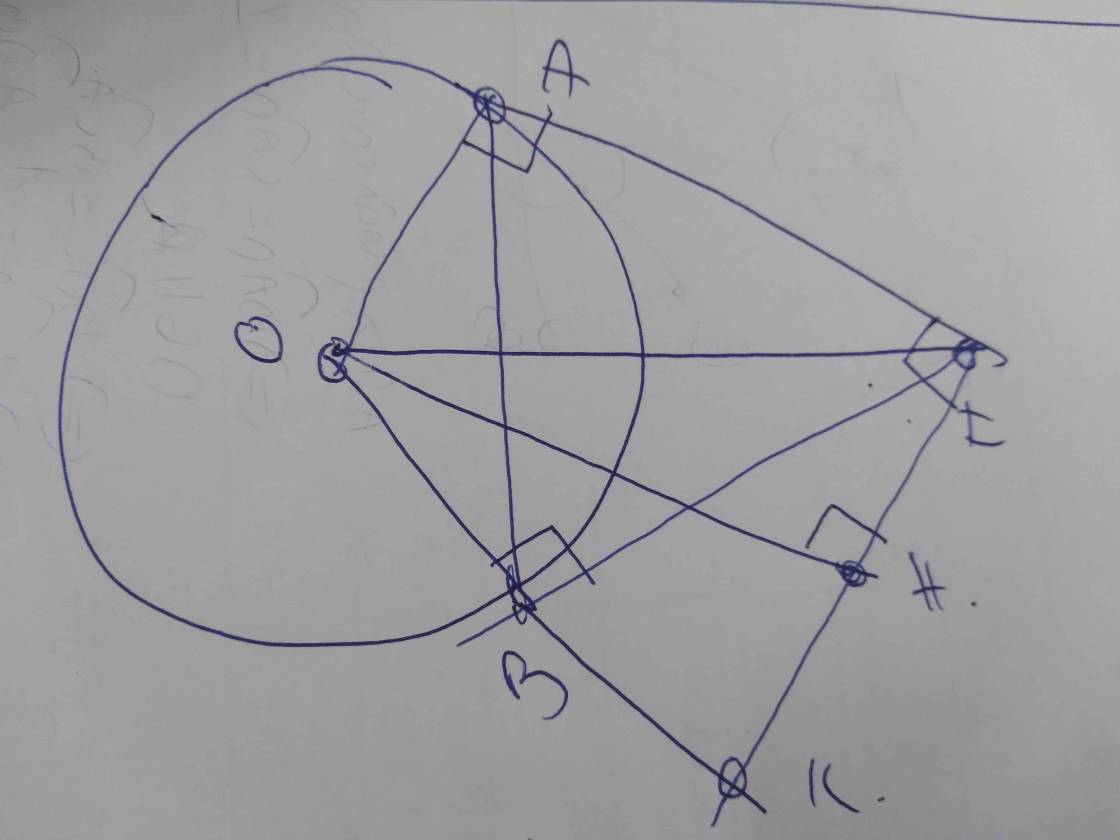
Cho hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại I. Đường thẳng đi qua I và vuông góc với IA cắt OB tại K. Chứng minh
a) IK//OA
b) Tam giác IOK cân
giúp câu b vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
27 tháng 10 2023
Đúng(0)
Những câu hỏi liên quan
CM
28 tháng 4 2017
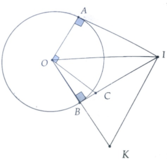
a, Chứng minh C là trực tâm của tam giác OIK. Từ đó suy ra KC ⊥ OI tại H
b, IA=12cm
Chứng minh ΔKOI cân tại K
Đặt KO = KI = x (x>0)
Có I K 2 = I B 2 + B K 2
Hay x 2 = 12 2 + x - 9 2
=> x = 12,5 => IK = 12,5cm
29 tháng 12 2023
a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC và AO là phân giác của góc BAC và OA là phân giác của góc BOC
Ta có: \(\widehat{KAO}+\widehat{COA}=90^0\)(ΔCAO vuông tại C)
\(\widehat{KOA}+\widehat{BOA}=\widehat{BOK}=90^0\)
mà \(\widehat{COA}=\widehat{BOA}\)
nên \(\widehat{KAO}=\widehat{KOA}\)
=>ΔKAO cân tại K
b:
Xét ΔOBA vuông tại B có \(sinBAO=\dfrac{OB}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAO}=30^0\)
Ta có: ΔBOA vuông tại B
=>\(\widehat{BAO}+\widehat{BOA}=90^0\)
=>\(\widehat{BOA}=90^0-30^0=60^0\)
Xét ΔOBI có OB=OI và \(\widehat{BOI}=60^0\)
nên ΔOBI đều
=>OI=OB=1/2OA=R
=>I là trung điểm của OA
ΔKAO cân tại K
mà KI là trung tuyến
nên KI vuông góc với OI
=>KI là tiếp tuyến của (O)
18 tháng 12 2021
b: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC
21 tháng 3 2020
+ Ta có: AB là tiếp tuyến của (O)(gt)
nên AB\(\perp\)OB
=> \(\Delta\)OBA vuông tại B(đpcm)
+ Xét \(\Delta\)OAK Có A1=A2 ( 1 ) (t/c 2 tiếp tuyến cắt nhau)
OK // AB => A1 = O1 ( 2 ) (so le trong)
Từ (1, 2) => (đpcm)
b, Xét \(\Delta\)AKO cân tại K (cmt)
IA = IO (=R)
=> KI là đường trung tuyến \(\Delta\)AKO
=> KI cũng là đường cao
=> KI\(\perp\)AO hay KM \(\perp\)IO
Vậy KM là tiếp tuyến của (O) (đpcm)
c, MI = MB ; KI = KC ; AB = AC ( t/c 2 tiếp tuyến cắt nhau )
Xét \(\Delta\)ABO vuông tại B (cmt)
AD định lí Py ta go ta cs :
AO2 =AB2 + OB2
AB2 = AO2 - OB2
AB2 = 4R2 - R2
AB = \(R\sqrt{3}\)
dễ rùi tự lm tiếp