Cho hệ bất phương trình sau:
\(\left\{ \begin{array}{l}x - y < 3\left( 1 \right)\\x + 2y > - 2\left( 2 \right)\end{array} \right.\)
a) Mỗi bát phương trình (1) và (2) có là bất phương trình bậc nhất hai ẩn không?
b) Chỉ ra một nghiệm chung của hai bất phương trình (1) và (2) trong hệ trên.

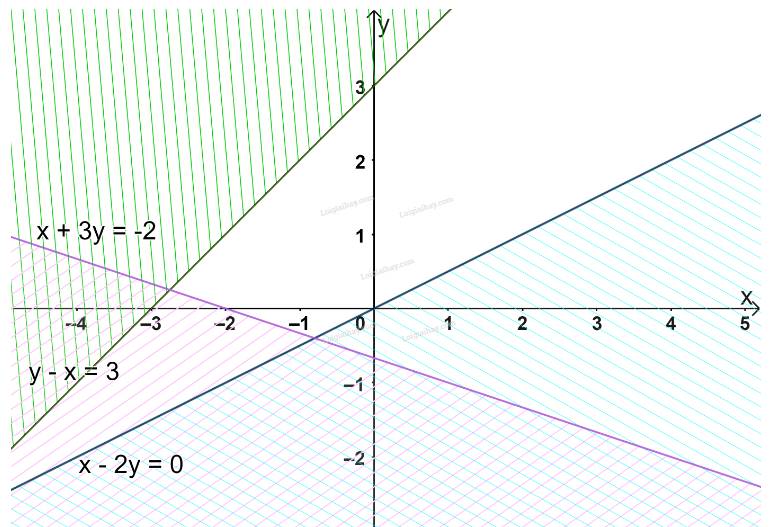

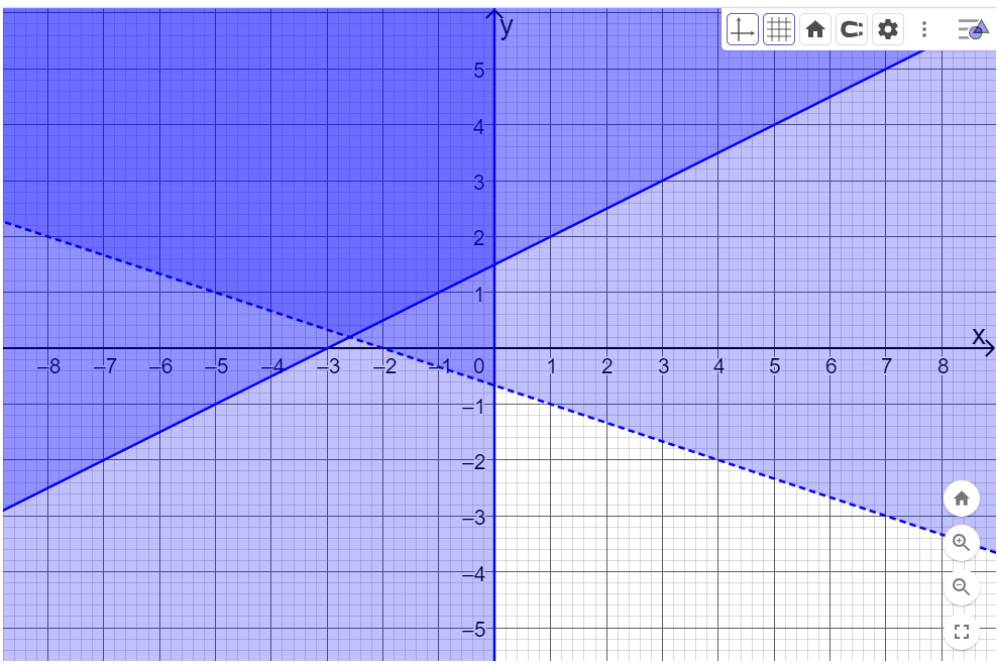
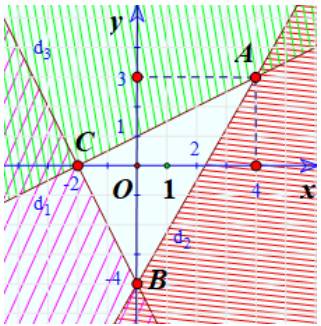
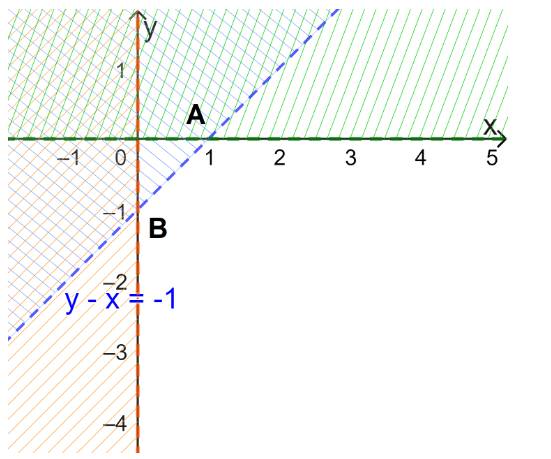
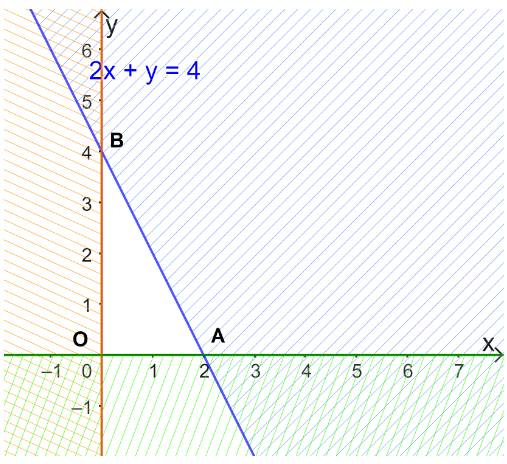
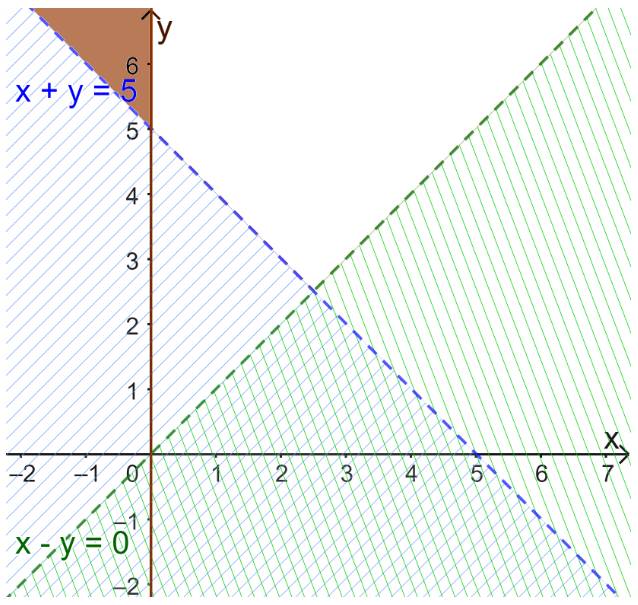
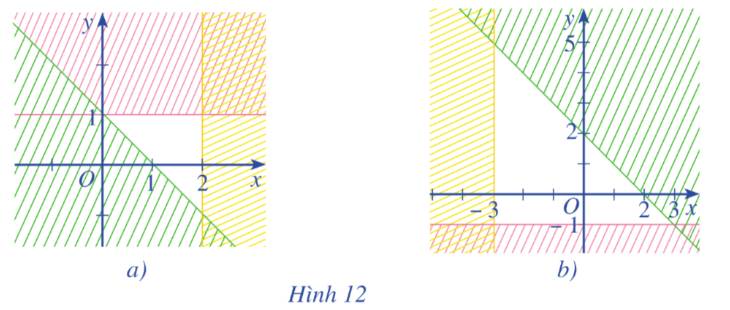
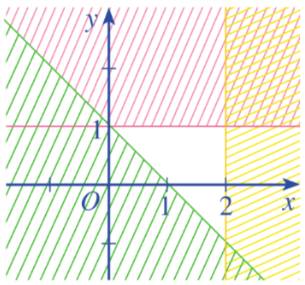
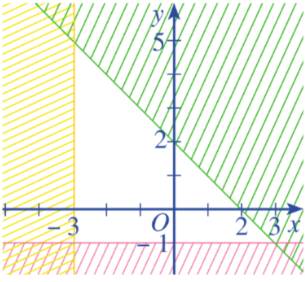
a) Hai bất phương trình bài cho là bất phương trình bậc nhất hai ẩn.
b) (1; 1) là một nghiệm chung của hai BPT (1) và (2) vì:
Thay x=1;y=1 vào (1) ta được: 1-1<3 (Luôn đúng)
Thay x=1; y=1 vào (2) ta được: 1+2.1>-2 (Luôn đúng)