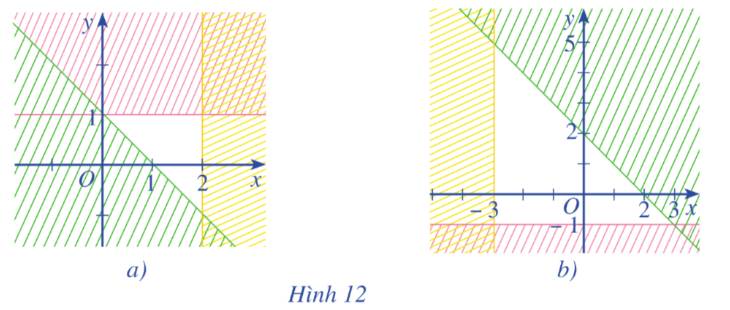
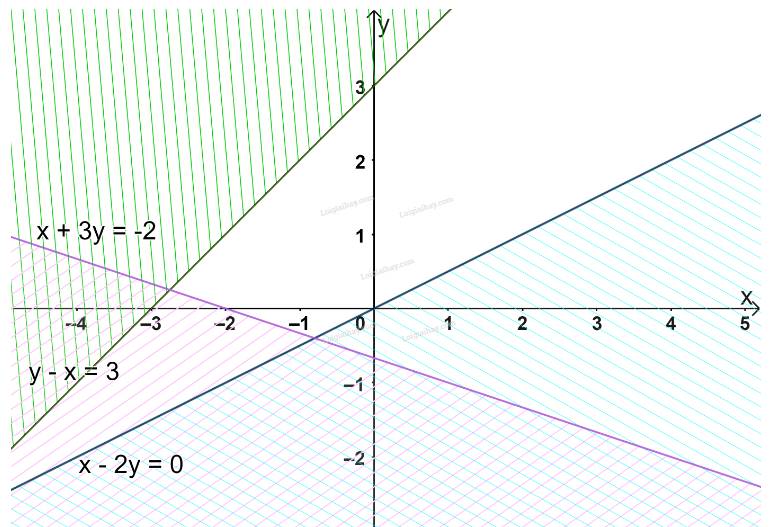
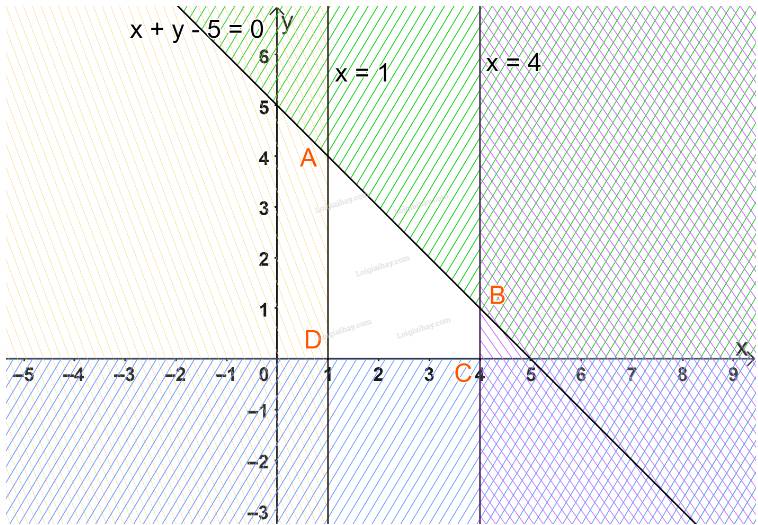
Miền không bị gạch ở mỗi Hình 12a, 12b là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?
a) \(\left\{ \begin{array}{l}x + y \le 2\\x \ge - 3\\y \ge - 1\end{array} \right.\)
b) \(\left\{ \begin{array}{l}y \le x\\x \le 0\\y \ge - 3\end{array} \right.\)
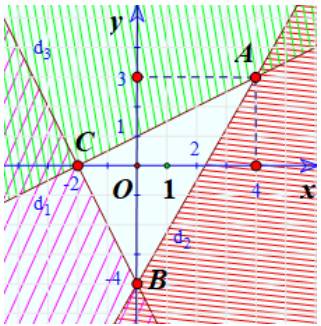
c) \(\left\{ \begin{array}{l}y \ge - x + 1\\x \le 2\\y \le 1\end{array} \right.\)

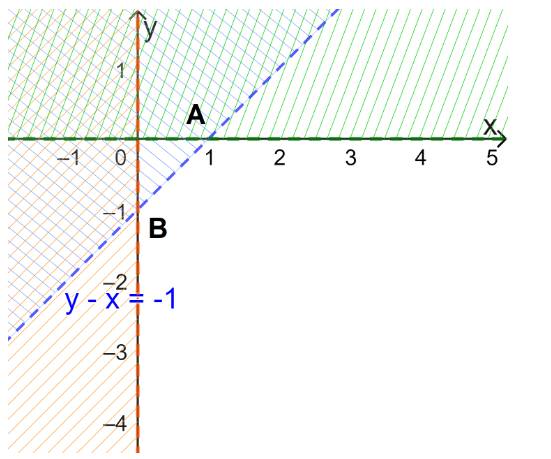
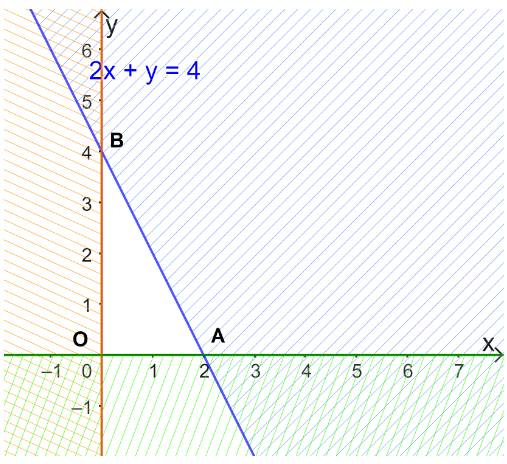
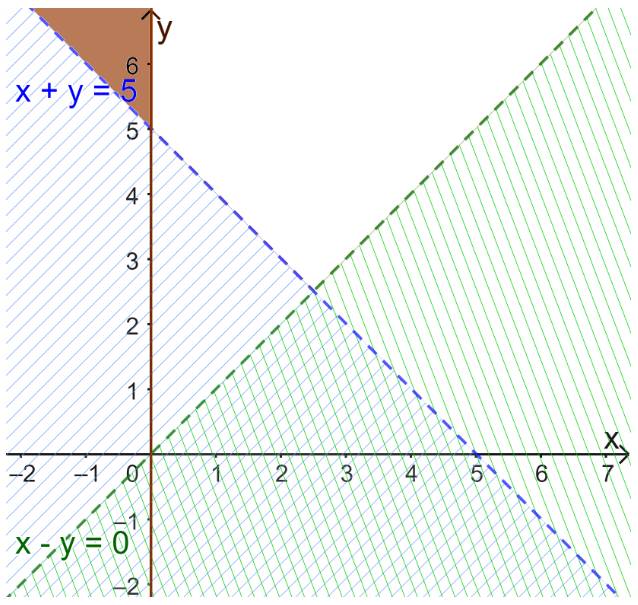
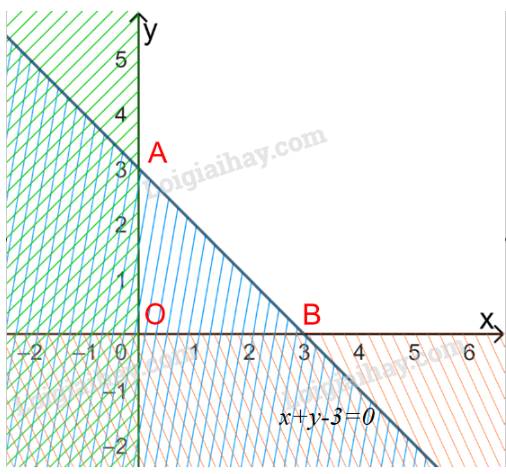

Hình 12a
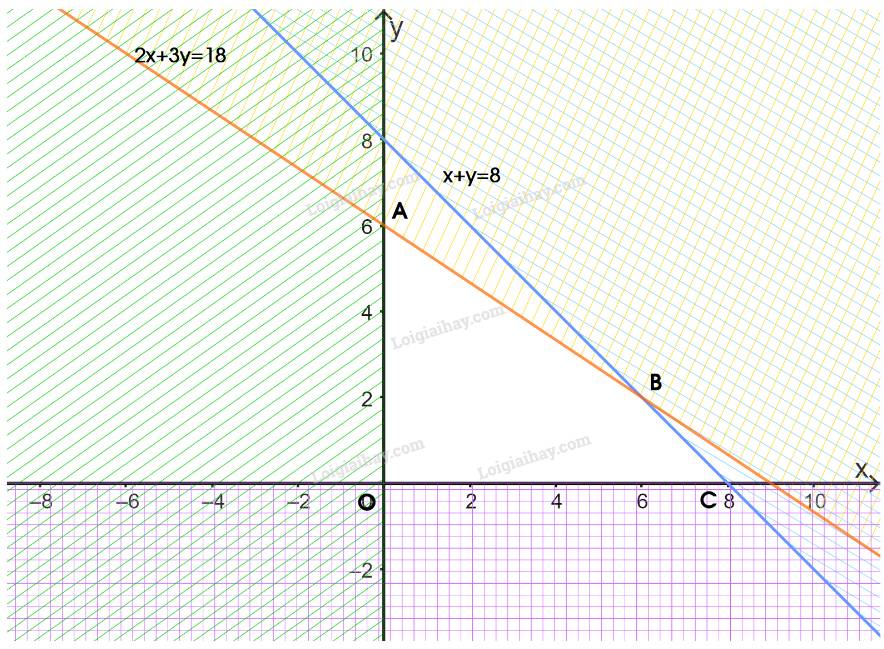
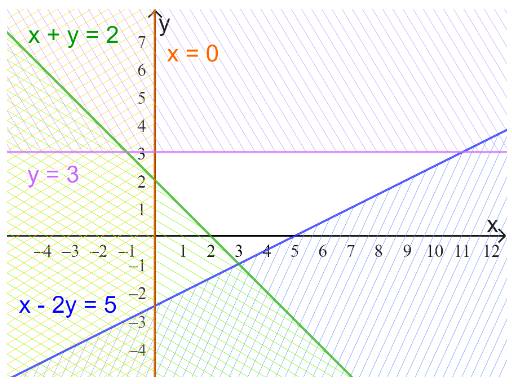
Ta thấy các đường thẳng trên hình là \(y = 1;x = 2;y = - x + 1\)
Từ các phương trình trên thì ta chọn luôn là câu c mà không cần xét tiếp.
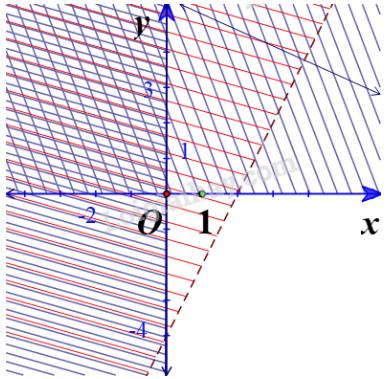
Hình 12b.
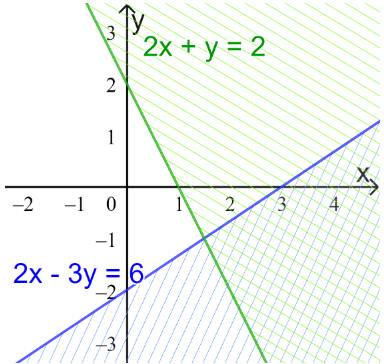
Ta thấy các đường thẳng trên hình là \(y = - 1;x = - 3;x + y = - 2\)
Từ các phương trình trên thì ta chọn luôn là câu a mà không cần xét tiếp