Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm tọa độ tâm và bán kính của đường tròn đó.
a) \({x^2} + {y^2} - 6x - 8y + 21 = 0\)
b) \({x^2} + {y^2} - 2x + 4y + 2 = 0\)
c) \({x^2} + {y^2} - 3x + 2y + 7 = 0\)
d) \(2{x^2} + 2{y^2} + x + y - 1

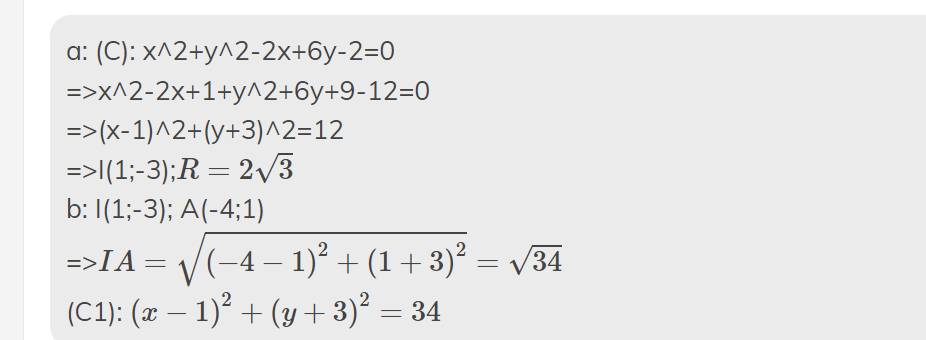
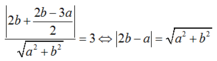
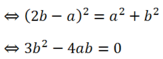

a) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = 3,b = 4,c = 21\)
Ta có \({a^2} + {b^2} - c = 9 + 16 - 21 = 4 > 0\). Vậy đây là phương trình đường tròn có tâm là \(I(3;4)\) và có bán kính \(R = \sqrt 4 = 2\)
b) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = 1,b = - 2,c = 2\)
Ta có \({a^2} + {b^2} - c = 1 + 4 - 2 = 3 > 0\). Vậy đây là phương trình đường tròn có tâm là \(I(1; - 2)\) và có bán kính \(R = \sqrt 3 \)
c) Phương trình đã cho có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \(a = \frac{3}{2},b = - 1,c = 7\)
Ta có \({a^2} + {b^2} - c = \frac{9}{4} + 1 - 7 = - \frac{{15}}{4} < 0\). Vậy đây không là phương trình đường tròn.
d) Phương trình không có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) nên phương trình đã cho không là phương trình đường tròn.