viết các công thức biến đổi căn thức bậc hai?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{A^2}=\left|A\right|\)
\(\sqrt{AB}=\sqrt{A}\sqrt{B}\)
\(\sqrt{\frac{A}{B}}=\frac{\sqrt{A}}{\sqrt{B}}\)
\(\sqrt{A^2B}=\left|A\right|\sqrt{B}\)
\(A\sqrt{B}=\sqrt{A^2B}\)
\(A\sqrt{B}=-\sqrt{A^2B}\)
\(\sqrt{\frac{A}{B}}=\frac{1}{\left|B\right|}\sqrt{AB}\)
\(\frac{A}{\sqrt{B}}=\frac{A\sqrt{B}}{B}\)
\(\frac{C}{\sqrt{A}\pm B}=\frac{C\left(\sqrt{A}-+B\right)}{A-B^2}\)
\(\frac{C}{\sqrt{A}\pm\sqrt{B}}=\frac{C\left(\sqrt{A}-+\sqrt{B}\right)}{A-B}\)
1. \(\sqrt{A^2}=\left|A\right|\)
2. \(\sqrt{A.B}=\sqrt{A}.\sqrt{B}\left(A\ge0;b\ge0\right)\)
3. \(\sqrt{\frac{A}{B}}=\frac{\sqrt{A}}{\sqrt{B}}\left(A\ge0;B\ge0\right)\)
4. \(\sqrt{A^2.B}=\sqrt{A^2}.\sqrt{B}=\left|A\right|.\sqrt{B}\left(B\ge0\right)\)
5. \(A\sqrt{B}\orbr{\begin{cases}\sqrt{A^2B}\left(A\ge0;B\ge0\right)\\\sqrt{A^2.B}\left(A< 0;B\ge0\right)\end{cases}}\)

\(a,\dfrac{5}{3\sqrt{8}}=\dfrac{5\sqrt{8}}{24};\dfrac{2}{\sqrt{b}}=\dfrac{2\sqrt{b}}{b}\\ b,\dfrac{5}{5-2\sqrt{3}}=\dfrac{5\left(5+2\sqrt{3}\right)}{13}=\dfrac{25+10\sqrt{3}}{12}\\ \dfrac{2a}{1-\sqrt{a}}=\dfrac{2a\left(1+\sqrt{a}\right)}{1-a}\\ c,\dfrac{4}{\sqrt{7}+\sqrt{5}}=\dfrac{4\left(\sqrt{7}-\sqrt{5}\right)}{2}=2\sqrt{7}-2\sqrt{5}\\ \dfrac{6a}{2\sqrt{a}-\sqrt{b}}=\dfrac{6a\left(2\sqrt{a}+\sqrt{b}\right)}{2a-b}=\dfrac{12a\sqrt{a}+6a\sqrt{b}}{2a-b}\)


Trục căn thức ở mẫu của biểu thức sau :
1 phần 1 cộng căn bậc hai cộng căn bậc ba (sr mik ko bt viết)


1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực
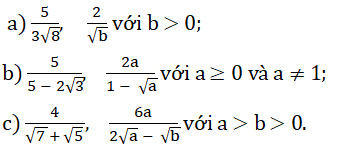
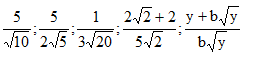
\(\sqrt{A^2}=\left|A\right|\)
\(\sqrt{A_1\cdot A_2\cdot...\cdot A_n}=\sqrt{A_1}\cdot\sqrt{A_2}\cdot...\cdot\sqrt{A_n}\)(ĐK: \(A_1>=0;A_2>=0;...;A_n>=0\))
\(\sqrt{\dfrac{A}{B}}=\dfrac{\sqrt{A}}{\sqrt{B}}\left(A>=0;B>0\right)\)
\(\sqrt{\dfrac{A}{B}}=\sqrt{\dfrac{AB}{B^2}}=\dfrac{\sqrt{AB}}{B}\left(A>=0;B>0\right)\)
\(\sqrt{A^2\cdot B}=\left|A\right|\cdot\sqrt{B}\left(B>=0\right)\)
\(A\cdot\sqrt{B}=\left[{}\begin{matrix}\sqrt{A^2\cdot B}\left(A>=0\right)\\-\sqrt{A^2\cdot B}\left(A< 0\right)\end{matrix}\right.\)