cho hình chóp S.ABCD đáy ABCD là hình chữ nhật, tâm O. Gọi H là trung điểm SC
a) Chứng minh BC ll (SAD)
b) Chứng minh AB ll (SCD)
c) Chứng minh OH ll (SAB)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 10 2023
a:
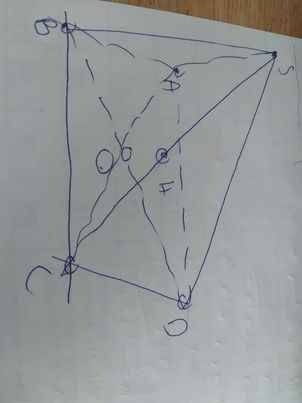
b: ABCD là hình chữ nhật
=>AB//CD và BC//AD
BC//AD
\(AD\subset\left(SAD\right)\)
BC không nằm trong mp(SAD)
Do đó: BC//(SAD)
c: AB//CD
\(CD\subset\left(SCD\right)\)
AB không nằm trong mp(SCD)
Do đó: AB//(SCD)
d: Xét ΔSAC có
O,H lần lượt là trung điểm của CA,CS
=>OH là đường trung bình của ΔSAC
=>OH//SA
OH//SA
\(SA\subset\left(SAB\right)\)
OH không nằm trong mp(SAB)
Do đó: OH//(SAB)
27 tháng 10 2023
a: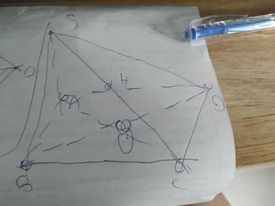 
b: BC//AD(ABCD là hình chữ nhật)
\(AD\subset\left(SAD\right)\)
BC không nằm trong mp(SAD)
Do đó: BC//(SAD)
c: AB//CD(ABCD là hình chữ nhật)
\(CD\subset\left(SCD\right)\)
AB không nằm trong mp(SCD)
Do đó: AB//(SCD)
d: Xét ΔSAC có
O,H lần lượt là trung điểm của CA,CS
=>OH là đường trung bình
=>OH//SA
OH//SA
\(SA\subset\left(SAB\right)\)
OH không nằm trong mp(SAB)
Do đó: OH//(SAB)
23 tháng 10 2023
a: Xét ΔSAC có
H,I lần lượt là trung điểm của SA,SC
=>HI là đường trung bình
=>HI//AC
mà \(AC\subset\left(ABCD\right)\); HI không thuộc (ABCD)
nên HI//(ABCD)
b: Xét ΔSCD có
I,K lần lượt là trung điểm của SC,SD
=>IK là đường trung bình
=>IK//CD
mà \(CD\subset\left(ABCD\right);IK\) không thuộc (ABCD)
nên IK//(ABCD)
c: IK//(ABCD)
HI//(ABCD)
\(IK,HI\subset\left(HIK\right)\)
Do đó: (HIK)//(ABCD)
17 tháng 11 2023
a: Xét ΔSAC có
I,H lần lượt là trung điểm của SC,SA
=>IH là đường trung bình của ΔSAC
=>IH//AC
IH//AC
AC\(\subset\)(ABCD)
IH không nằm trong mp(ABCD)
Do đó: IH//(ABCD)
b: XétΔSCD có
I,K lần lượt là trung điểm của SC,SD
=>IK là đường trung bình của ΔSCD
=>IK//CD
IK//CD
CD\(\subset\)(ABCD)
IK không nằm trong mp(ABCD)
Do đó: IK//(ABCD)
c: IK//(ABCD)
HI//(ABCD)
IK,HI nằm trong mp(HIK)
Do đó: (HIK)//(ABCD)
d: (HIK)//(ABCD)
=>BD//(HIK)
23 tháng 10 2023
a: ABCD là hình chữ nhật tâm O
=>O là trung điểm chung của AC và BD
Xét ΔASC có
O,E lần lượt là trung điểm của AC,AS
=>OE là đường trung bình
=>OE//SC
mà SC\(\subset\left(SCD\right)\) và OE không thuộc (SCD)
nên OE//(SCD)
b: Xét ΔBSD có
\(\dfrac{BO}{BD}=\dfrac{BF}{BS}=\dfrac{1}{2}\)
nên OF//SD
=>OF//(SDC)
c: OE//(SDC)
OF//(SDC)
\(OE,OF\subset\left(OEF\right)\)
Do đó: (OEF)//(SCD)
