Cho tam giác ABC vuông tại a, vẽ đường cao AH. Biết AB=6,5cm BH=2,5cm tính độ dài các đoạn thẳng AH, HC, BC, AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>BC=10(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC
=>AH*10=6*8=48
=>AH=4,8(cm)
ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\CH\cdot CB=CA^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}BH=\dfrac{6^2}{10}=3,6\left(cm\right)\\CH=\dfrac{8^2}{10}=6,4\left(cm\right)\end{matrix}\right.\)

Áp dụng ĐL Pytago vào tam giác ABC vuông tại A ta có :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=\sqrt{36}=6\left(cm\right)\)
Có diện tích tam giác ABC \(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}AB.AC\Leftrightarrow AH.BC=AB.AC\)
\(\Leftrightarrow AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=\frac{48}{10}=4,8\left(cm\right)\)
Áp dụng ĐL Pytago vào tam giác ABH vuông tại H ta có :
\(BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=\sqrt{12,96}=3,6\left(cm\right)\)
Áp dụng ĐL Pytago vào tam giác ACH vuông tại H ta có :
\(CH=\sqrt{AC^2-AH^2}=\sqrt{8^2-4,8^2}=\sqrt{40,96}=6,4\left(cm\right)\)

Ta có:
\(AH^2=BH.HC\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{3^2}{4}=\dfrac{9}{4}\left(cm\right)\)
\(BC=BH+HC=4+\dfrac{9}{4}=9\left(cm\right)\)
\(AB=\sqrt{BH.BC}=\sqrt{4.9}=6\left(cm\right)\)
\(AC=\sqrt{CH.BC}=\sqrt{\dfrac{9}{4}.9}=\dfrac{9}{2}\left(cm\right)\)

a, HB = 1,8cm; CH = 3,2cm; AH = 2,4cm; AC = 4cm
b, AB = 65cm; AC = 156cm; BC = 169cm; BH = 25cm
c, AB = 5cm; BC = 13cm; BH = 25/13cm; CH = 144/13cm
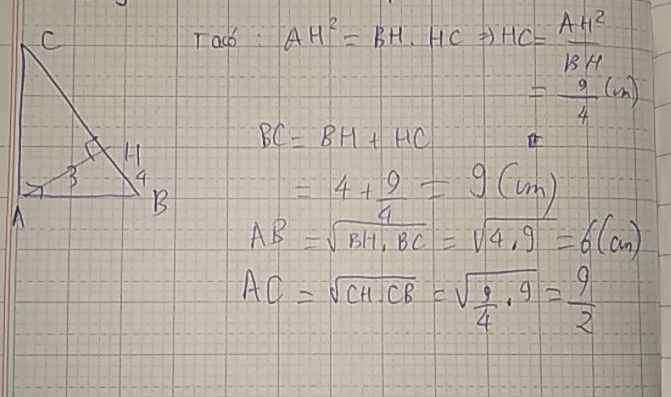

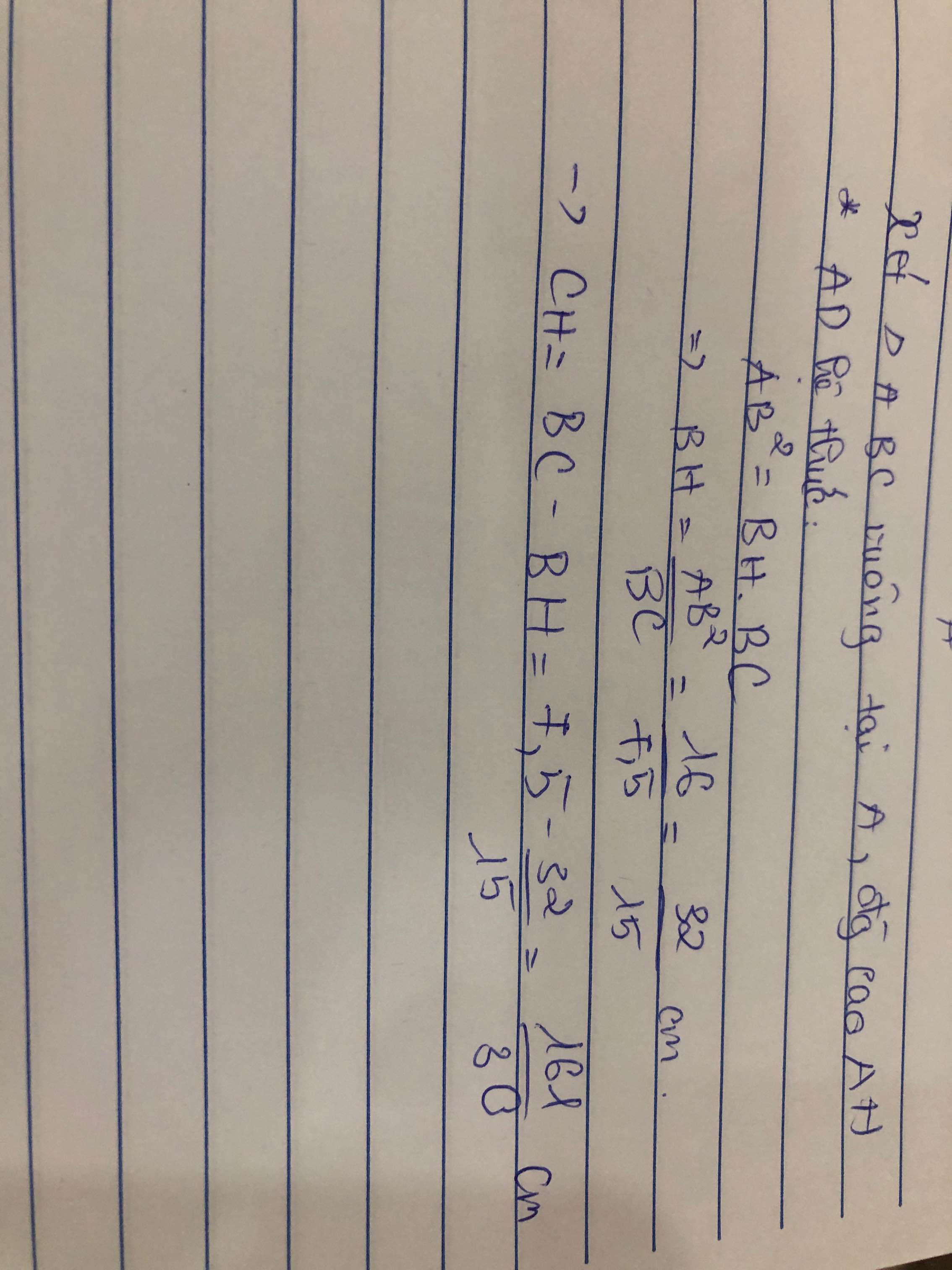
Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
=>\(BC\cdot2,5=6,5^2\)
=>\(BC=\dfrac{6.5^2}{2.5}=16,9\left(cm\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA=\sqrt{6.5^2-2.5^2}=6\left(cm\right)\)
HC+HB=BC
=>HC+2,5=16,9
=>HC=14,4(cm)
ΔAHC vuông tại H
=>\(HA^2+HC^2=AC^2\)
=>\(AC^2=14,4^2+6^2=243,86\)
=>AC=15,6(cm)
Cảm ơn bạn nhiều!