a) Các phân số đảo ngược là:

\(\dfrac{5}{8}\rightarrow\dfrac{8}{5};\dfrac{3}{4}\rightarrow\dfrac{4}{3};\dfrac{1}{2}\rightarrow\dfrac{2}{1}=2\)

b) \(\dfrac{3}{7}:\dfrac{5}{8}=\dfrac{3}{7}\times\dfrac{8}{5}=\dfrac{24}{35}\)

\(\dfrac{8}{7}:\dfrac{3}{4}=\dfrac{8}{7}\times\dfrac{4}{3}=\dfrac{32}{21}\)

\(\dfrac{1}{3}:\dfrac{1}{2}=\dfrac{1}{3}\times2=\dfrac{2\times1}{3}=\dfrac{2}{3}\)

a) \(\dfrac{20}{12}\)          b) \(\dfrac{15}{15}\)          c) \(\dfrac{24}{42}\)

d) \(\dfrac{26}{39}\)          e) \(\dfrac{0}{8}\)          g) \(\dfrac{15}{3}\)

a) \(\dfrac{15}{3}\)

b)\(\dfrac{15}{15}\)

c) \(\dfrac{24}{42}\)

d) \(\dfrac{26}{39}\)

e)\(\dfrac{0}{8}\)

f) \(\dfrac{15}{15}\)

a) \(A=\left\{x\in N|x=3k+1;0\le k\le3;k\in z\right\}\)

b) \(B=\left\{x\in Q^+|x=\dfrac{k}{k^2-1};2\le k\le6;k\in N\right\}\)

a) Ta có \(A=\dfrac{n-5}{n-3}=\dfrac{n-3-2}{n-3}=1-\dfrac{2}{n-3}\). Để \(A\inℤ\) thì \(\dfrac{2}{n-3}\inℤ\) hay \(n-3\) là ước của 2. Suy ra \(n-3\in\left\{\pm1;\pm2\right\}\). 

Nếu \(n-3=1\Rightarrow n=4\); \(n-3=-1\Rightarrow n=2\); \(n-3=2\Rightarrow n=5\); \(n-3=-2\Rightarrow n=1\). Vậy để \(A\inℤ\) thì \(n\in\left\{1;2;4;5\right\}\)

 \(A=\dfrac{n+4}{n+1}\) làm tương tự.

b) Dễ thấy các số ở mẫu có thể viết dưới dạng:

\(10=1+2+3+4=\dfrac{4\left(4+1\right)}{2}=\dfrac{4.5}{2}\)

\(15=1+2+3+4+5=\dfrac{5\left(5+1\right)}{2}=\dfrac{5.6}{2}\)

\(21=1+2+...+6=\dfrac{6\left(6+1\right)}{2}=\dfrac{6.7}{2}\)

...

\(120=1+2+...+15=\dfrac{15\left(15+1\right)}{2}=\dfrac{15.16}{2}\)

Do đó \(A=\dfrac{2}{4.5}+\dfrac{2}{5.6}+\dfrac{2}{6.7}+...+\dfrac{2}{15.16}\) 

\(A=2\left(\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{15.16}\right)\)

\(A=2\left(\dfrac{5-4}{4.5}+\dfrac{6-5}{5.6}+\dfrac{7-6}{6.7}+...+\dfrac{16-15}{15.16}\right)\)

\(A=2\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{15}-\dfrac{1}{16}\right)\)

\(A=2\left(\dfrac{1}{4}-\dfrac{1}{16}\right)\)

\(A=\dfrac{3}{8}\)

a) \(\dfrac{2}{5}\times?=\dfrac{3}{10}\)

\(?=\dfrac{3}{10}:\dfrac{2}{5}=\dfrac{3}{4}\)

b) \(\dfrac{1}{8}:?=\dfrac{1}{5}\)

\(?=\dfrac{1}{8}:\dfrac{1}{5}=\dfrac{5}{8}\)

a: Phân số cần tìm là: \(\dfrac{3}{10}:\dfrac{2}{5}=\dfrac{3}{10}\cdot\dfrac{5}{2}=\dfrac{15}{20}=\dfrac{3}{4}\)

b: Phân số cần tìm là \(\dfrac{1}{8}:\dfrac{1}{5}=\dfrac{5}{8}\)

Tham khảo:

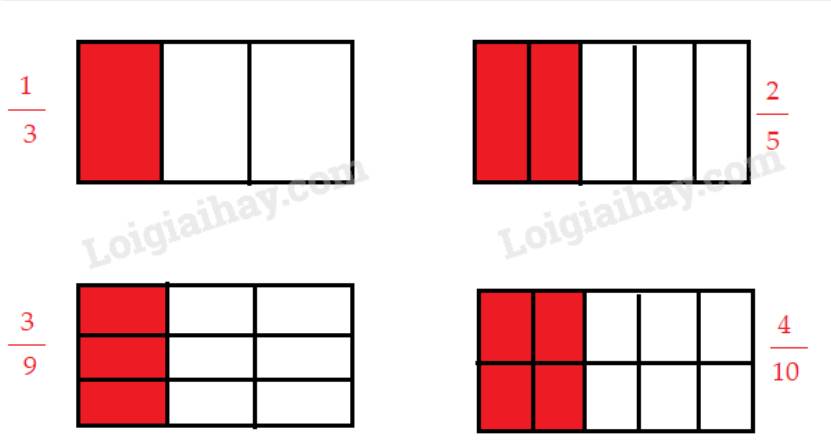
Như vậy,\(\dfrac{2}{5} = \dfrac{4}{{10}}\)

\(\dfrac{1}{3} = \dfrac{3}{9}\)

a,A,C,D

b,C

a) Câu A;D

b) Câu C

Bài 1:

a) 

\(\dfrac{1}{2}=\dfrac{1\times6}{2\times6}=\dfrac{6}{12}\)

\(\dfrac{2}{3}=\dfrac{2\times4}{3\times4}=\dfrac{8}{12}\)

\(\dfrac{3}{4}=\dfrac{3\times3}{4\times3}=\dfrac{9}{12}\)

b)

\(\dfrac{1}{3}=\dfrac{1\times15}{3\times15}=\dfrac{15}{45}\)

\(\dfrac{2}{15}=\dfrac{2\times3}{15\times3}=\dfrac{6}{45}\)

\(\dfrac{4}{45}\) (giữ nguyên)

c)

\(\dfrac{1}{8}=\dfrac{1\times3}{8\times3}=\dfrac{3}{24}\)

\(\dfrac{2}{3}=\dfrac{2\times8}{3\times8}=\dfrac{16}{24}\)

\(\dfrac{5}{2}=\dfrac{5\times12}{2\times12}=\dfrac{60}{24}\)

d)

\(\dfrac{2}{7}=\dfrac{2\times4}{7\times4}=\dfrac{8}{28}\)

\(\dfrac{9}{4}=\dfrac{9\times7}{4\times7}=\dfrac{63}{28}\)

\(\dfrac{5}{28}\) (giữ nguyên)

Bài 2:

a)

\(4=\dfrac{4}{1}=\dfrac{4\times12}{1\times12}=\dfrac{48}{12}\)

\(\dfrac{9}{4}=\dfrac{9\times3}{4\times3}=\dfrac{27}{12}\)

b)

\(\dfrac{5}{8}=\dfrac{5\times30}{8\times30}=\dfrac{150}{240}\)

\(\dfrac{25}{30}=\dfrac{5}{6}=\dfrac{5\times40}{6\times40}=\dfrac{200}{240}\)

\(2=\dfrac{2}{1}=\dfrac{2\times240}{1\times240}=\dfrac{480}{240}\).

giúp mình với ạ!