AI GIÚP GIẢI CÂU 3 VSSSS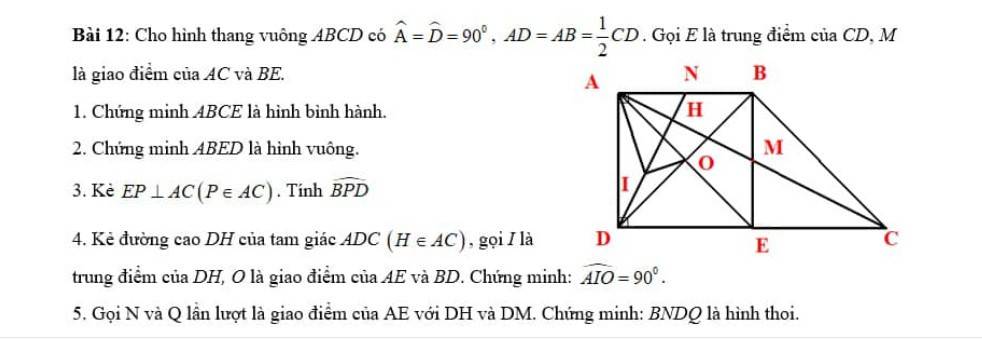
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(x+20)100+|y+4|=0
\(\Rightarrow\orbr{\begin{cases}x+20=0\\y+4=0\end{cases}\Rightarrow}\orbr{\begin{cases}x=-20\\y=-4\end{cases}}\)
Vậy x=-20;y=-4


Tôi đá bóng : một động tác
Mẹ tôi là áo : một việc
Nó rải rác quanh hồ : tần suất
Tôi yêu đường : thành phần của mía, có vị ngọt
Chiếu tướng ! : một hành động ( một nước đi trong cờ vua )
Tôi cày điểm : ( làm việc )


\(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{z}{5}=\dfrac{6x}{9}=\dfrac{6y}{8}=\dfrac{6z}{30}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{6x}{9}=\dfrac{6y}{8}=\dfrac{6z}{30}=\dfrac{6\left(x+y+z\right)}{9+8+30}=\dfrac{6.20}{47}=\dfrac{120}{47}\\ \Rightarrow x=\dfrac{120}{47}.3:2=\dfrac{180}{47}\\ \Rightarrow y=\dfrac{120}{47}.4:3=\dfrac{160}{47}\\ \Rightarrow z=\dfrac{120}{47}.5=\dfrac{600}{47}\)
Bạn xem xem cách này có đúng không nha!


39. It is raining so we can't go to the beach.
40. If they liked this house, they would buy it.
41. Hurry up or we will be late.
42. They take pride of their school uniform.
43. Why don't we go out for a walk?

`a,b,c` lập thành CSC `=>a+c=2b`
Thay `a+c=2b` vào `a+b+c=15` có: `2b+b=15<=>b=5`
`=>a+c=2.5=10=>a=10-c`
Thay `b=5` vào `1/a+1/b+1/c=71/105` có:
`1/a+1/5+1/c=71/105`
`<=>1/a+1/c=10/21`
`<=>21a+21c=10ac` `(1)`
Thay `a=10-c` vào `(1)` có: `21(10-c)+21c=10(10-c)c`
`<=>[(c=3),(c=7):}=>[(a=7),(a=3):}`
KL: `[(a=7;b=5;c=3),(a=3;b=5;c=7):}`
 lm 3 câu mik vssss
lm 3 câu mik vssss
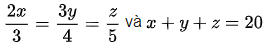



1: \(AB=\dfrac{1}{2}CD\)
\(CE=ED=\dfrac{CD}{2}\)
Do đó: AB=CE=ED
Xét tứ giác ABCE có
AB//CE
AB=CE
Do đó: ABCE là hình bình hành
2: Xét tứ giác ABED có
AB//ED
AB=ED
Do đó: ABED là hình bình hành
Hình bình hành ABED có AB=AD
nên ABED là hình thoi
Hình thoi ABED có \(\widehat{BAD}=90^0\)
nên ABED là hình vuông
3: Gọi giao điểm của AE và BD là L
ABED là hình vuông
=>AE=BD và AE vuông góc với BD tại trung điểm của mỗi đường
=>L là trung điểm chung của AE và BD và AE=BD
=>\(LA=LE=LB=LD=\dfrac{BD}{2}=\dfrac{AE}{2}\)
ΔAPE vuông tại P
mà PL là đường trung tuyến
nên \(PL=\dfrac{AE}{2}=\dfrac{BD}{2}\)
Xét ΔBPD có
PL là đường trung tuyến
\(PL=\dfrac{BD}{2}\)
Do đó: ΔBPD vuông tại P
=>\(\widehat{BPD}=90^0\)