
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


7:
a: a>b
=>a+2>b+2
b: a>b
=>a-2>b-2
c: a>b
=>2*a>2b
d: a>b
=>-2a<-2b

Bài 4. c)
\(P\left(x\right)=x^3+3x^2+mx+8\) chia hết cho \(x+4\) suy ra \(P\left(-4\right)=0\)
khi đó \(\left(-4\right)^3+3.\left(-4\right)^2+m.\left(-4\right)+8=0\Leftrightarrow m=-2\).

Thực hiện phép chia:
(2a^2+a-7):(x-2) được dư là 3
Để 2a^2+a-7 chia hết cho a-2
thì 3 chia hết cho a-2
=>a-2€Ư(3)
=>a-2=1<=>a=3(nhận)
a-2=-1<=>a=1(nhận)
a-2=3<=>a=5(nhận)
a-2=-3<=>a=-1(nhận)
Vây, a€{3;1;5;-1} để (2a^2+a-7)chia hết cho (a-2) l

Câu 2:
Gọi số sách Nam mua được là x(sách)(Điều kiện: \(x\in Z^+\))
Số tập Nam mua được là: x+3(tập)
Theo đề, ta có phương trình:
\(12000x+5000\left(x+3\right)=83000\)
\(\Leftrightarrow12000x+5000x+15000=83000\)
\(\Leftrightarrow17000x=68000\)
hay x=4(thỏa ĐK)
Vậy: Bạn Nam mua được 4 quyển sách và 7 cuốn tập


\(\left(x-\sqrt{2}\right)+3.\left(x^2-2\right)=0\)
\(\Leftrightarrow\left(x-\sqrt{2}\right)+3.\left(x^2-\sqrt{2}^2\right)=0\)
\(\Leftrightarrow\left(x-\sqrt{2}\right)+3.\left(x-\sqrt{2}\right).\left(x+\sqrt{2}\right)=0\)
\(\Leftrightarrow\left(x-\sqrt{2}\right).\left[1+3.\left(x+\sqrt{2}\right)\right]=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-\sqrt{2}=0\\1+3.\left(x+\sqrt{2}\right)=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\sqrt{2}\\x+\sqrt{2}=-\frac{1}{3}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\sqrt{2}\\x=-\frac{1}{3}-\sqrt{2}\end{cases}}}}\)
Vậy ...

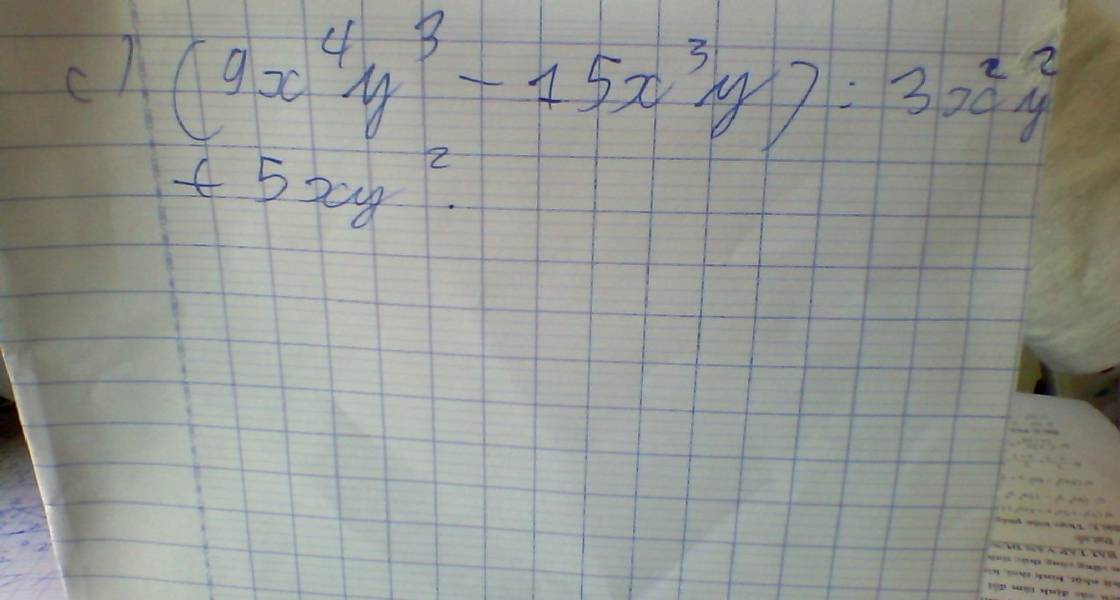
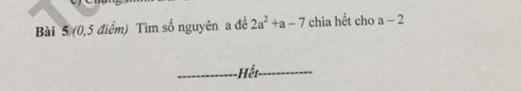

 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
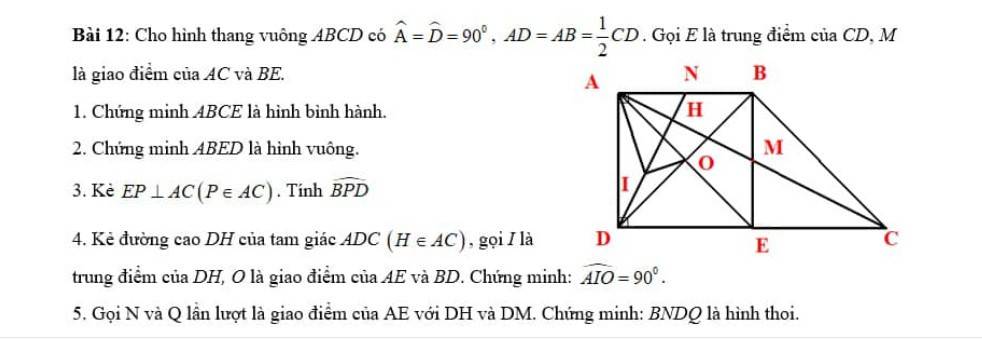
1: \(AB=\dfrac{1}{2}CD\)
\(CE=ED=\dfrac{CD}{2}\)
Do đó: AB=CE=ED
Xét tứ giác ABCE có
AB//CE
AB=CE
Do đó: ABCE là hình bình hành
2: Xét tứ giác ABED có
AB//ED
AB=ED
Do đó: ABED là hình bình hành
Hình bình hành ABED có AB=AD
nên ABED là hình thoi
Hình thoi ABED có \(\widehat{BAD}=90^0\)
nên ABED là hình vuông
3: Gọi giao điểm của AE và BD là L
ABED là hình vuông
=>AE=BD và AE vuông góc với BD tại trung điểm của mỗi đường
=>L là trung điểm chung của AE và BD và AE=BD
=>\(LA=LE=LB=LD=\dfrac{BD}{2}=\dfrac{AE}{2}\)
ΔAPE vuông tại P
mà PL là đường trung tuyến
nên \(PL=\dfrac{AE}{2}=\dfrac{BD}{2}\)
Xét ΔBPD có
PL là đường trung tuyến
\(PL=\dfrac{BD}{2}\)
Do đó: ΔBPD vuông tại P
=>\(\widehat{BPD}=90^0\)