71x64+32x(-7)-13x32
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a.
$21\times 23-3\times 7\times (-17)$
$=21\times 23-21\times (-17)$
$=21\times 23+21\times 17=21\times (23+17)=21\times 40$
$=840$
b.
$42\times 3-7\times [(-34)+18]$
$=7\times 18-7\times (-16)$
$=7\times 18+7\times 16=7\times (18+16)=7\times 34=238$
c.
$=142\times 32+32\times (-7)-13\times 32$
$=32\times (142-7-32)=32\times 103=3296$
d.
$=13\times [(23-17)-(23+17)]$
$=13\times (23-17-23-17)=13\times (-34)=-442$

\(=71.32.2-32.\left(-7\right)-32.\left(-11\right)\)
\(=142.32+32.7+32.11\)
\(=32.\left(142+7+11\right)\)
\(=32.160=5120\)
CHÚC BẠN HỌC TỐT..........

Điều kiện xác định: x ≠ ±3; x ≠ -7/2.
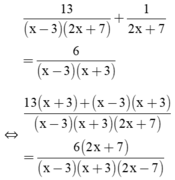
⇒ 13(x + 3) + (x – 3)(x + 3) = 6(2x + 7)
⇔ 13x + 39 + x2 – 9 = 12x + 42
⇔ x2 + x – 12 = 0
⇔ x2 +4x – 3x – 12 = 0
⇔ x(x + 4) – 3(x + 4) = 0
⇔ (x – 3)(x + 4) = 0
⇔ x – 3 = 0 hoặc x + 4 = 0
x – 3 = 0 ⇔ x = 3 (không thỏa mãn đkxđ)
x + 4 = 0 ⇔ x = -4 (thỏa mãn đkxđ).
Vậy phương trình có tập nghiệm S = {-4}.

13 x - 3 2 x + 7 + 1 2 x + 7 = 6 x 2 - 9 Đ K X Đ : x ≠ ± 3 v à x ≠ - 7 2 ⇔ 13 x + 3 x 2 - 9 2 x + 7 + x 2 - 9 2 x + 7 x 2 - 9 = 6 2 x + 7 x 2 - 9 2 x + 7
⇔ 13(x + 3) + x 2 – 9 = 6(2x + 7)
⇔ 13x + 39 + x 2 – 9 = 12x + 42
⇔ x 2 + x – 12 = 0
⇔ x 2 – 3x + 4x – 12 = 0
⇔ x(x – 3) + 4(x – 3) = 0
⇔ (x + 4)(x – 3) = 0
⇔ x + 4 = 0 hoặc x – 3 = 0
x + 4 = 0 ⇔ x = -4 (thỏa mãn)
x – 3 = 0 ⇔ x = 3 (loại)
Vậy phương trình có nghiệm x = -4.

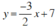
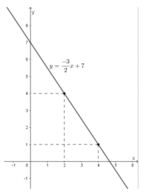
+ x = 2 thì y = 4. Vậy điểm (2; 4) thuộc đồ thị hàm số.
+ x = 4 thì y = 1. Vậy điểm (4; 1) thuộc đồ thị hàm số.

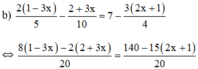
⇔ 8(1 – 3x) – 2(2 + 3x) = 140 – 15(2x + 1)
⇔ 8 – 24x – 4 – 6x = 140 – 30x – 15
⇔ 4 – 30x = 125 – 30x
⇔ 0x = 121 (vô lý)
Vậy phương trình vô nghiệm.

Hướng dẫn: Lấy logarit cơ số 2 cả hai vế
Phương trình đã cho có hai nghiệm phân biệt đều thỏa mãn điều kiện
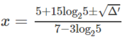

x + 1 3 + 3 2 x + 1 4 = 2 x + 3 x + 1 6 + 7 + 12 x 12 ⇔ x + 1 3 + 6 x + 3 4 = 5 x + 3 6 + 7 + 12 x 12
⇔ 4(x + 1) + 3(6x + 3) = 2(5x + 3) + 7 + 12x
⇔ 4x + 4 + 18x + 9 = 10x + 6 + 7 + 12x
⇔ 4x + 18x – 10x – 12x = 6 + 7 – 4 – 9
⇔ 0x = 0
Phương trình có vô số nghiệm.
\(71\cdot64+32\cdot\left(-7\right)-13\cdot32\)
\(=32\cdot2\cdot71+32\cdot\left(-7\right)+32\cdot\left(-13\right)\)
\(=32\left(142-7-13\right)\)
\(=32\cdot122=3904\)