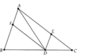
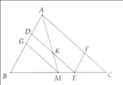
Cho tam giác ABC có phân giác AD, trung tuyến AM. QUa M kẻ đường thẳng song song với AB, cắt AD tại E. QUa D kẻ đường thẳng song song với AC, cắt AM tại K. Chứng minh tam giác AEK vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi Bx là tia đối của tia BA. Lấy E trên AC sao cho AB = AE
Xét tam giác BAD=EAD c-g-c => BD = DE và DEC = CBx
Trong tam giác ABC, BAC + ABC + ACB = 180 => ACB = 180 - BAC - ABC => ACB < 180 - ABC
Ta có DBx + ABC = 180 (hai góc kề bù) => DBx = 180 - ABC
=>ACB < DBx => ACB < DEC => Trong tam giác DEC, DC > DE (Quan hệ giữa góc và cạnh)
Vậy BD < DC

Cm: a) Ta có: BA ⊥⊥AC (gt)
HD // AB (gt)
=> HD ⊥⊥AC => ˆHDA=900HDA^=900
Ta lại có: AC ⊥⊥AB (gt)
HE // AC (gt)
=> HE ⊥⊥AB => ˆHEA=900HEA^=900
Xét tứ giác AEHD có: ˆA=ˆAEH=ˆHDA=900A^=AEH^=HDA^=900
=> AEHD là HCN => AH = DE
b) Gọi O là giao điểm của AH và DE
Ta có: AEHD là HCN => OE = OH = OD = OA
=> t/giác OAD cân tại O => ˆOAD=ˆODAOAD^=ODA^ (1)
Xét t/giác ABC vuông tại A có AM là đường trung tuyến
-> AM = BM = MC = 1/2 BC
=> t/giác AMC cân tại M => ˆMAC=ˆCMAC^=C^
Ta có: ˆB+ˆC=900B^+C^=900 (phụ nhau)
ˆC+ˆHAC=900C^+HAC^=900 (phụ nhau)
=> ˆB=ˆHACB^=HAC^ hay ˆB=ˆOADB^=OAD^ (2)
Từ (1) và (2) => ˆODA=ˆBODA^=B^
Gọi I là giao điểm của MA và ED
Xét t/giác IAD có: ˆIAD+ˆIDA+ˆAID=1800IAD^+IDA^+AID^=1800 (tổng 3 góc của 1 t/giác)
=> ˆAID=1800−(IAD+ˆIDA)AID^=1800−(IAD+IDA^)
hay ˆAID=1800−(ˆB+ˆC)=1800−900=900AID^=1800−(B^+C^)=1800−900=900
=> AM⊥DEAM⊥DE(Đpcm)
c) (thiếu đề)

Chứng minh tứ giác AEDF là hình thoi
Þ EF là phân giác của A E D ^