Giúp em giải hẳn ra như tự luận ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 50 thì bạn nhóm cặp lại tan1*tan89*tan2*tan88*...*tan45
thì bạn sẽ thấy là tan1*tan89=tan2*tan88=...=tan45=1
=>D
Câu 51 thì bạn nhóm cặp lại \(sin^288^0;sin^22^0\); sin2860 và sin240;...;sin244 độ và sin2 46 độ thì bạn sẽ thấy từng cặp đó có tổng bằng 1
Và có 22 cặp như vậy nên đáp án là C

Câu 18:
Ta có: \(3\sqrt{8a}+\dfrac{1}{4}\sqrt{\dfrac{32a}{25}}-\dfrac{a}{\sqrt{3}}\cdot\sqrt{\dfrac{3}{2a}}-\sqrt{2a}\)
\(=6\sqrt{2a}-\sqrt{2a}+\dfrac{1}{4}\cdot\dfrac{4\sqrt{2a}}{5}-\dfrac{a}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{\sqrt{2a}}\)
\(=5\sqrt{2a}+\dfrac{1}{5}\sqrt{2a}-\dfrac{1}{2}\sqrt{2a}\)
\(=\dfrac{47}{10}\sqrt{2a}\)
Chọn C
Câu 18
\(=3\sqrt{4}.\sqrt{2a}+\frac{1}{4}\sqrt{\frac{16}{25}}.\sqrt{2a}-\sqrt{\frac{a^2}{3}}.\sqrt{\frac{3}{2a}}-\sqrt{2a}\)
\(=6\sqrt{2a}+\frac{1}{5}\sqrt{2a}-\sqrt{\frac{a}{2}}-\sqrt{2a}\)
\(=6\sqrt{2a}+\frac{1}{5}\sqrt{2a}-\sqrt{\frac{1}{4}}.\sqrt{2a}-\sqrt{2a}\)
\(=6\sqrt{2a}+\frac{1}{5}\sqrt{2a}-\frac{1}{2}\sqrt{2a}-\sqrt{2a}=\frac{47}{10}\sqrt{2a}\)
Đáp án C.




Câu 3:
\(n_{CO_2}=\dfrac{0,44}{44}=0,01\left(mol\right)\)
\(n_{H_2O}=\dfrac{0,18}{18}=0,01\left(mol\right)\)
Bảo toàn C: nC(A) = 0,01 (mol)
Bảo toàn H: nC(A) = 2.0,01 = 0,02 (mol)
=> \(n_O=\dfrac{0,3-0,01.12-0,02.1}{16}=0,01\left(mol\right)\)
nC : nH : nO = 0,01 : 0,02 : 0,01 = 1:2:1
=> CTHH: (CH2O)n
Có\(n_{O_2}=\dfrac{0,32}{32}=0,01\left(mol\right)=>M_A=\dfrac{0,3}{0,01}=30\left(g/mol\right)\)
=> n = 1
=> CTHH: CH2O
Câu 4:
\(n_{NO_2}=\dfrac{5,152}{22,4}=0,23\left(mol\right)\)
PTHH: Cu + 4HNO3 --> Cu(NO3)2 + 2NO2 + 2H2O
_____a---------------------------------->2a
Fe + 6HNO3 --> Fe(NO3)3 + 3NO2 + 3H2O
b---------------------------------->3b
=> \(\left\{{}\begin{matrix}64a+56b=5,36\\2a+3b=0,23\end{matrix}\right.=>\left\{{}\begin{matrix}a=0,04\\b=0,05\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}\%Cu=\dfrac{0,04.64}{5,36}.100\%=47,76\%\\\%Fe=\dfrac{0,05.56}{5,36}.100\%=52,24\%\end{matrix}\right.\)

Do d' là ảnh của d qua phép tịnh tiến nên d' cùng phương với d
\(\Rightarrow\) Phương trình d' có dạng: \(x-2y+c=0\)
Chọn \(A\left(-1;0\right)\) là 1 điểm thuộc d
Gọi \(A'\left(x';y'\right)\) là ảnh của A qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow A'\in d'\)
\(\left\{{}\begin{matrix}x'=-1+\left(-1\right)=-2\\y'=0+3=3\end{matrix}\right.\) \(\Rightarrow A'\left(-2;3\right)\)
Thế vào pt d':
\(-2-2.3+c=0\Rightarrow c=8\)
Vậy pt d' có dạng: \(x-2y+8=0\)


Lời giải:
HPT \(\Leftrightarrow \left\{\begin{matrix} xy+4x-5y-20=xy+x-4y-4\\ xy-3x+y-3=xy-2x-y+2\end{matrix}\right.\)
\( \Leftrightarrow \left\{\begin{matrix} 3x-y=16\\ -x+2y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{37}{5}\\ y=\frac{31}{5}\end{matrix}\right.\)
Khi đó: \(m+2n=\frac{37}{5}+2.\frac{31}{5}=\frac{99}{5}\)
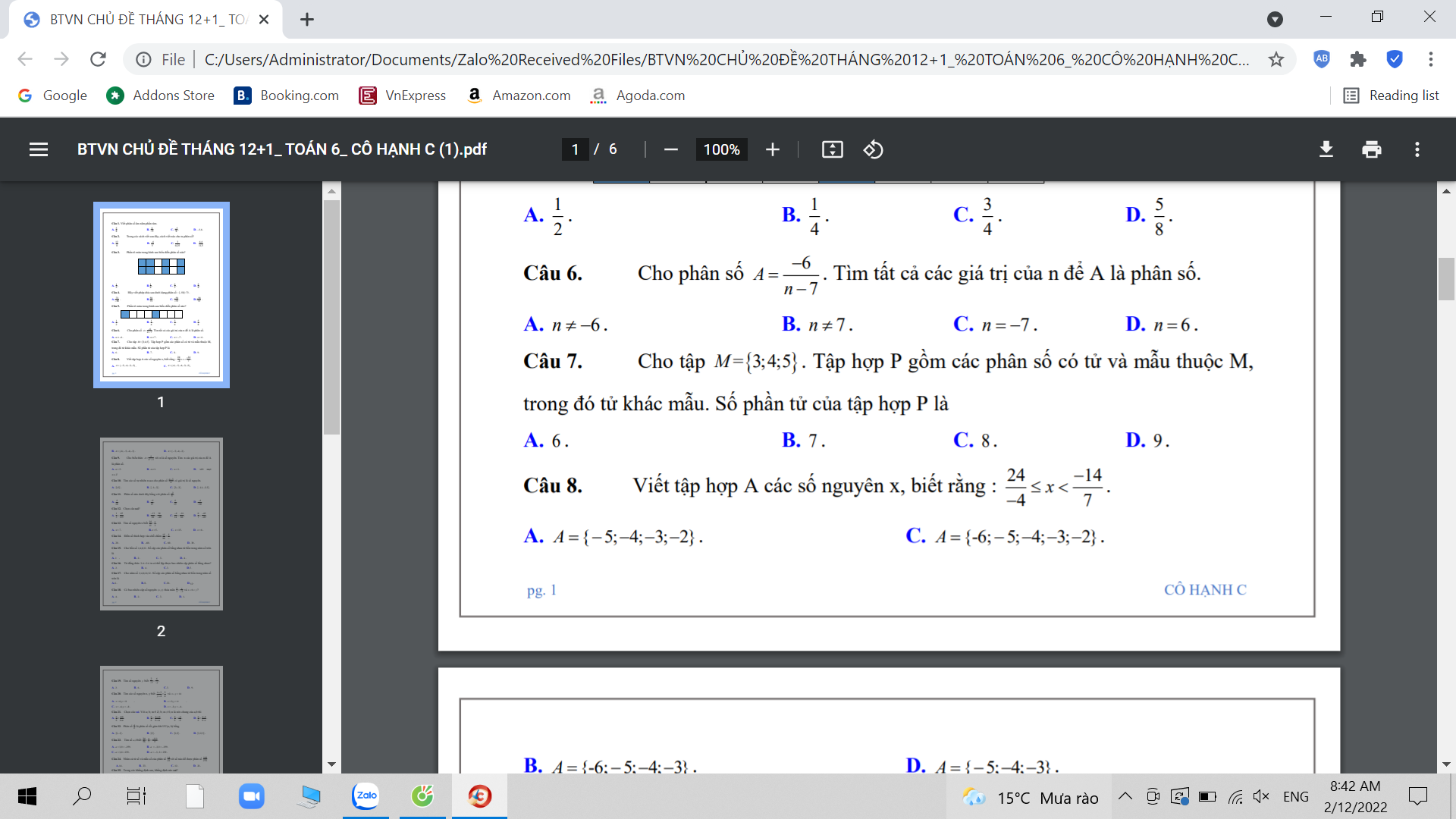 mọi người giúp em với ạ em đang cần gấp!!
mọi người giúp em với ạ em đang cần gấp!!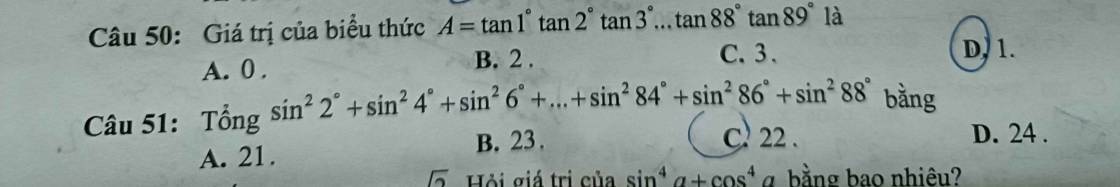






câu nào bạn ?
câu 6,7,8