VẼ HỘ MÌNH HÌNH ĐỀ NÀY Ạ
Cho đường tròn (O) bán kính R = 2 cm. Điểm A nằm ngoài đường tròn. Từ A vẽ các tiếp tuyến AB,AC với đường tròn (B,C là các tiếp điểm). AO cắt BC tại D. a) Cmr 4 điểm A,B,O,C cùng thuộc 1 đường tròn và OA là trung trực của BC b) Vẽ đk BE của đường tròn (O), AE cắt đt (O) tại điểm thứ hai F. Gọi G là trung điểm của EF. Đt OG cắt đt BC tại H. Tính tích OA.OD và cm OA.OD=OG.OH c) CM EH là tiếp tuyến của đt (O)




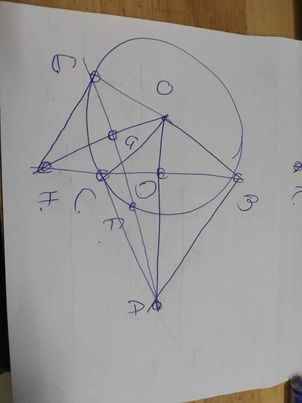
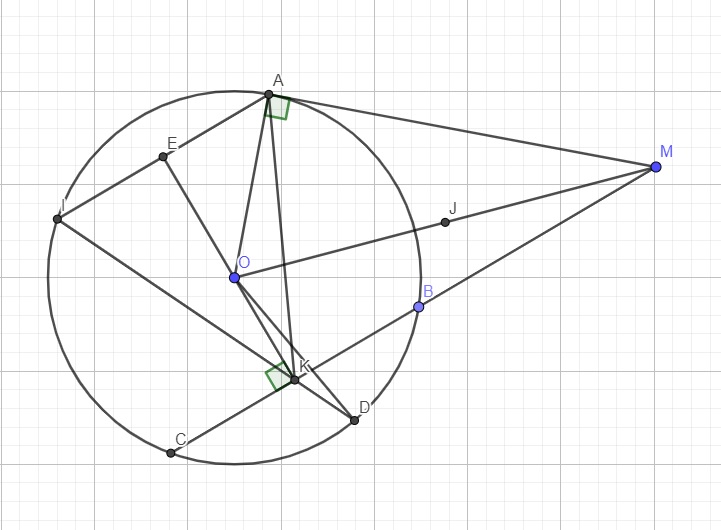
Hình khó nhìn quá bạn vẽ lại cho mình với