Chọn C.

Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.

Cách giải:

tuổi con HN là :

50 : ( 1 + 4 ) = 10 ( tuổi )

tuổi bố HN là :

50 - 10 = 40 ( tuổi )

hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi

ta có sơ đồ : bố : |----|----|----|

                  con : |----| hiệu 30 tuổi

tuổi con khi đó là :

 30 : ( 3 - 1 ) = 15 ( tuổi )

số năm mà bố gấp 3 tuổi con là :

 15 - 10 = 5 ( năm )

       ĐS : 5 năm

mình nha

1: double a,b,c

3: double b

4: double a,c

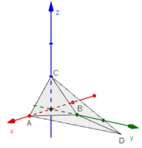
a) Cách 1:

Phương trình đoạn chắn (ABC) là:

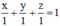 hay x + y + z – 1 = 0.

Thay tọa độ điểm D(-2; 1; -1) ta được: (-2) + 1 + (-1) – 1 = -3 ≠ 0

⇒ D không nằm trong (ABC)

⇒ A, B, C, D không đồng phẳng

⇒ A, B, C, D là bốn đỉnh của một tứ diện.

Cách 2:

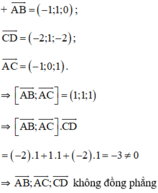
⇒ A, B, C, D không đồng phẳng

⇒ A, B, C, D là bốn đỉnh của hình tứ diện.

trả lời lẹ cho tui cấy

\(\frac{1}{a}\)<\(\frac{1}{b}\)

Ta có:

\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=0\)

\(\Leftrightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2=0\)

\(\Leftrightarrow\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+2.\left(\dfrac{1}{ab}+\dfrac{1}{ac}+\dfrac{1}{bc}\right)=0\)

\(\Leftrightarrow2.\left(\dfrac{1}{ab}+\dfrac{1}{ac}+\dfrac{1}{bc}\right)=-\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)\)

Mà \(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}>0\)

\(\Rightarrow2\left(\dfrac{1}{ab}+\dfrac{1}{ac}+\dfrac{1}{bc}\right)< 0\)

\(\Leftrightarrow\dfrac{1}{ab}+\dfrac{1}{ac}+\dfrac{1}{bc}< 0\left(đpcm\right)\)

(Dấu"=" không xảy ra bạn nhé)

Thanks bạn

Câu 6:C

Câu 8:C

Câu 9:Tìm phần bù của B trong A có nghĩa là tìm A\B

Ý D

Câu 6: C

Câu 8: C

Câu 9: D

\(\left(\dfrac{1}{a}-1\right)\left(\dfrac{1}{b}-1\right)\left(\dfrac{1}{c}-1\right)=\left(\dfrac{1-a}{a}\right)\left(\dfrac{1-b}{b}\right)\left(\dfrac{1-c}{c}\right)\)

\(=\left(\dfrac{b+c}{a}\right)\left(\dfrac{a+c}{b}\right)\left(\dfrac{a+b}{c}\right)\ge\dfrac{2\sqrt{bc}}{a}.\dfrac{2\sqrt{ac}}{b}.\dfrac{2\sqrt{ab}}{c}=8\) (đpcm)

Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)