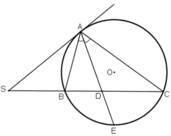
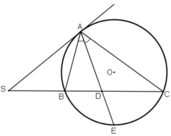
Từ S nằm ngoài (O), vẽ 2 tiếp tuyến SA,SA' và cát tuyến SBC với (O) (B nằm giữa SC)a) phân giác góc BAC cắt BC tại D, cắt (O) tại E. so sánh SA với SDb) OE cắt BS tại G, AA' cắt BC tại F, cắt SO tại H.c/m SH.SO=SG.SFc) c/m SD2 = SG.SFd) Biết SB=a, BC =2a/3. Tính...
Đọc tiếp
Từ S nằm ngoài (O), vẽ 2 tiếp tuyến SA,SA' và cát tuyến SBC với (O) (B nằm giữa SC)
a) phân giác góc BAC cắt BC tại D, cắt (O) tại E. so sánh SA với SD
b) OE cắt BS tại G, AA' cắt BC tại F, cắt SO tại H.c/m SH.SO=SG.SF
c) c/m SD2 = SG.SF
d) Biết SB=a, BC =2a/3. Tính SF
là góc có đỉnh nằm bên trong đường tròn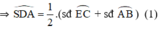
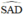là góc tạo bởi tiếp tuyến AS và dây AE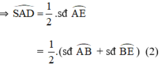
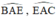lần lượt là các góc nội tiếp chắn các cung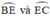 
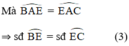
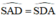
là góc có đỉnh nằm bên trong đường tròn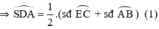
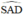là góc tạo bởi tiếp tuyến AS và dây AE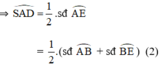
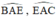lần lượt là các góc nội tiếp chắn các cung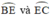 
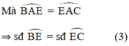
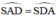
a.
Do AE là phân giác \(\Rightarrow\widehat{BAE}=\widehat{CAE}\Rightarrow sđ\stackrel\frown{BE}=sđ\stackrel\frown{CE}\)
\(\widehat{SAE}\) là góc tạo bởi tiếp tuyến tại A và dây AE \(\Rightarrow\widehat{SAE}=\dfrac{1}{2}sđ\stackrel\frown{AE}\) (1)
\(\widehat{SDA}\) là góc có đỉnh nằm trong đường tròn
\(\Rightarrow\widehat{SDA}=\dfrac{1}{2}\left(sđ\stackrel\frown{AB}+sđ\stackrel\frown{CE}\right)\) \(=\dfrac{1}{2}\left(sđ\stackrel\frown{AB}+sđ\stackrel\frown{BE}\right)=\dfrac{1}{2}sđ\stackrel\frown{AE}\) (2)
(1);(2) \(\Rightarrow\widehat{SAE}=\widehat{SDA}\Rightarrow\Delta SAD\) cân tại S
\(\Rightarrow SA=SD\)
b.
Ta có \(SA=SA'\) (t/c hai tiếp tuyến cắt nhau); \(OA=OA'=R\)
\(\Rightarrow SO\) là trung trực của AA'
Hay SO vuông góc AA' tại H hay tam giác SHF vuông tại H
\(sđ\stackrel\frown{BE}=sđ\stackrel\frown{CE}\Rightarrow E\) là điểm chính giữa cung BC
OE là đường kính đi qua đi qua điểm chính giữa cung BC \(\Rightarrow OE\perp BC\)
Hay tam giác SGO vuông tại G
Xét hai tam giác SGO và SHF có:
\(\left\{{}\begin{matrix}\widehat{SGO}=\widehat{SHF}=90^0\\\widehat{GSO}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta SGO\sim\Delta SHF\left(g.g\right)\)
\(\Rightarrow\dfrac{SO}{SF}=\dfrac{SG}{SH}\Rightarrow SH.SO=SG.SF\)
c.
SA là tiếp tuyến tại A \(\Rightarrow\Delta SAO\) vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông SAO với đường cao AH:
\(SA^2=SH.SO\)
Mà theo chứng minh trên \(\left\{{}\begin{matrix}SD=SA\\SH.SO=SG.SF\end{matrix}\right.\)
\(\Rightarrow SD^2=SG.SF\)
d.
Do OE vuông góc BC tại G (theo cm câu b) \(\Rightarrow G\) là trung điểm BC
\(\Rightarrow BG=\dfrac{1}{2}BC=\dfrac{a}{3}\Rightarrow SG=SB+BG=\dfrac{4a}{3}\)
Xét hai tam giác SAB và SCA có:
\(\left\{{}\begin{matrix}\widehat{SAB}=\widehat{SCA}\left(\text{cùng chắn AB}\right)\\\widehat{CSA}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta SAB\sim\Delta SCA\left(g.g\right)\)
\(\Rightarrow\dfrac{SA}{SC}=\dfrac{SB}{SA}\Rightarrow SA^2=SB.SC=SB^2.\left(SB+BC\right)=\dfrac{5a^2}{3}\)
Theo đẳng thức câu c: \(SA^2=SD^2=SG.SF\)
\(\Rightarrow SF=\dfrac{SA^2}{SG}=\dfrac{5a}{4}\)