/A/=B trong đó A,B là các biểu thức đại số
Tìm điều kiện xác định
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 6:
ĐKXĐ: \(x\ne-\dfrac{1}{3}\)
Để \(\dfrac{9x+4}{3x+1}\in Z\) thì \(9x+4⋮3x+1\)
=>\(9x+3+1⋮3x+1\)
=>\(1⋮3x+1\)
=>\(3x+1\in\left\{1;-1\right\}\)
=>\(3x\in\left\{0;-2\right\}\)
=>\(x\in\left\{0;-\dfrac{2}{3}\right\}\)
mà x nguyên
nên x=0
Câu 2:
a: ĐKXĐ: \(x\notin\left\{2;-2;0\right\}\)
b: \(A=\left(\dfrac{1}{x+2}-\dfrac{2x}{4-x^2}+\dfrac{1}{x-2}\right)\cdot\dfrac{x^2-4x+4}{4x}\)
\(=\left(\dfrac{1}{x+2}+\dfrac{2x}{\left(x-2\right)\left(x+2\right)}+\dfrac{1}{x-2}\right)\cdot\dfrac{\left(x-2\right)^2}{4x}\)
\(=\dfrac{x-2+2x+x+2}{\left(x+2\right)\left(x-2\right)}\cdot\dfrac{\left(x-2\right)^2}{4x}\)
\(=\dfrac{4x\left(x-2\right)}{4x\left(x+2\right)}=\dfrac{x-2}{x+2}\)

a) Điều kiện : 3x2 – 12x ≠ 0; 3x3 – 12x = 3x(x2 – 4) = 3x(x – 2)(x + 2).
Vậy: x ≠ 0; x ≠ 2 và x ≠ -2.

\(a,đk\left(B\right):x\ne\pm3\\ B=\dfrac{3}{x-3}-\dfrac{6x}{9-x^2}+\dfrac{x}{x+3}\\ =\dfrac{3}{x-3}+\dfrac{6x}{x^2-9}+\dfrac{x}{x+3}\\ =\dfrac{3\left(x+3\right)+6x+x\left(x-3\right)}{x^2-9}\\ =\dfrac{3x+9+6x+x^2-3x}{x^2-9}\\ =\dfrac{x^2+6x+9}{x^2-9}\\ =\dfrac{\left(x+3\right)^2}{x^2-9}\\ =\dfrac{x+3}{x-3}\)
\(b,P=A.B\\ =\dfrac{x+1}{x+3}\times\dfrac{x+3}{x-3}\\ =\dfrac{x+1}{x-3}\)
\(c,\) Để P nguyên
\(\dfrac{x+1}{x-3}=1+\dfrac{4}{x-3}\)
=> \(x-3\inƯ\left(4\right)\)
\(Ư\left(4\right)=\left\{-1;1;2;-2;4;-4\right\}\)
\(=>x=\left\{2;4;5;1;7;-1\right\}\)

a) Để giá trị của \(\dfrac{2x^2+7}{3x+21}\) được xác định thì 3x + 21 \(\ne\) 0
=> 3(x+7) \(\ne\) 0
=> x+7 \(\ne\) 0
=> x \(\ne\) -7
Vậy để giá trị của biểu thức \(\dfrac{2x^2 +7}{3x+21}\) được xác định thì x \(\ne\) -7
b) Để giá trị của \(\dfrac{x+5}{-12+6}\) được xác định thì x \(\in\) R ( vì -12+6 \(\ne\) 0)

a) \(\sqrt{3x-4}\) xác định \(\Leftrightarrow3x-4\ge0\Leftrightarrow3x\ge4\Leftrightarrow x\ge\dfrac{4}{3}\)
b) \(\dfrac{1}{\sqrt{x-4}}\) xác định \(\Leftrightarrow x-4>0\Leftrightarrow x>4\)

\(a,ĐK:x\ne\pm1;x\ne0\\ M=\dfrac{1-x+2x}{\left(1+x\right)\left(1-x\right)}:\dfrac{1-x}{x}\\ M=\dfrac{x+1}{\left(x+1\right)\left(1-x\right)}\cdot\dfrac{x}{1-x}=\dfrac{x}{\left(1-x\right)^2}\\ b,ĐK:x\ge0;x\ne4\\ N=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ N=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
Tất cả đều phải tìm điều kiện

a) Ta có: x - 1 ≠ 0 ⇒ x ≠ 1
x2 - 1 = (x + 1)(x - 1) ≠ 0 ⇔ x ≠ -1 và x ≠ 1
x2 - 2x + 1 = (x - 1)2 ≠ 0 ⇔ x - 1 ≠ 0 ⇔ x ≠ 1
ĐKXĐ: x ≠ -1 và x ≠ 1

![]()
![]()
![]()
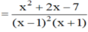
ĐKXĐ la B>=0 bn nhé