Mọi người giúp e bài này với ạ. E cảm ơn ạ
K
Khách
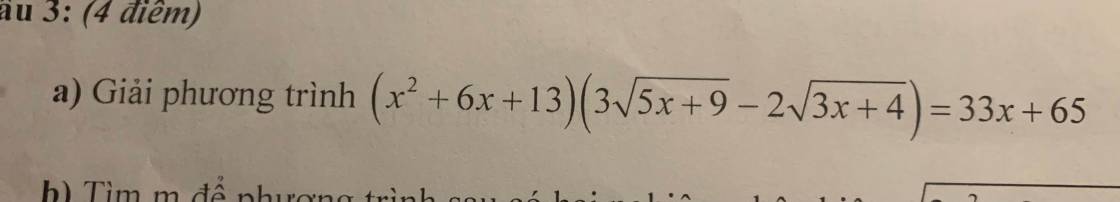
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
2
AH
Akai Haruma
Giáo viên
19 tháng 8 2021
Lời giải:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$|x+2020|+|x+2021|=|x+2020|+|-(x+2021)|$
$\geq |x+2020-(x+2021)|=1$
Vậy GTNN của biểu thức là $1$. Giá trị này đạt tại $(x+2020).-(x+2021)\geq 0$
$(x+2020)(x+2021)\leq 0$
$-2021\leq x\leq -2020$
TH
0
BT
3
DT
Đỗ Thanh Hải
CTVVIP
3 tháng 5 2021
1 Where did you go?
2 Who did you go with?
3 How did you get there?
4 What did you do during the day?
5 Did you have a good time?
MN
3 tháng 5 2021
1. Where did you go?
Where was you going?
2. Who did you go with?
Who was you going with?
3. How did you get there?
How was you getting there?
MN
2 tháng 10 2021
Em nên chia bài này ra làm 2, 3 nhé vì liền một lúc 4 đoạn như vậy mng sẽ nản hoặc khó để làm em nhé!
15 tháng 10 2021
Bài 5:
a) Do \(x,y\in N\)
\(\Rightarrow\left\{\left(x;y-2\right)\right\}\in\left\{\left(1;7\right),\left(7;1\right)\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(1;9\right),\left(7;3\right)\right\}\)
b) Do \(x,y\in N\)
\(\Rightarrow\left(x+1;y+5\right)\in\left\{\left(1;12\right),\left(2;6\right)\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(0;7\right),\left(1;1\right)\right\}\)
c) Do \(x,y\in N\)
\(\Rightarrow\left(x-1;2y+1\right)\in\left\{\left(18;1\right),\left(2;9\right),\left(6;3\right)\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(19;0\right),\left(3;4\right),\left(7;1\right)\right\}\)
ND
1
H
5 tháng 1 2022
bạn đăng tách ra tầm 10 câu mỗi lần đăng nha, chứ dài ntnay ngại làm lắm~
5 tháng 1 2022
e có tách 3 bài ra rồi ạ, phiền anh/chị/bạn giúp e với ạ, e cảm ơn ạ
ĐKXĐ: \(x\ge-\dfrac{4}{3}\)
\(\left(x^2+6x+13\right)\left(\dfrac{9\left(5x+9\right)-4\left(3x+4\right)}{3\sqrt{5x+9}+2\sqrt{3x+4}}\right)=33x+65\)
\(\Leftrightarrow\dfrac{\left(x^2+6x+9\right)\left(33x+65\right)}{3\sqrt{5x+9}+2\sqrt{3x+4}}=33x+65\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{65}{33}< -\dfrac{4}{3}\left(ktm\right)\\x^2+6x+9=3\sqrt{5x+9}+2\sqrt{3x+4}\left(1\right)\end{matrix}\right.\)
Xét (1)
\(\Leftrightarrow x^2+x+3\left(x+3-\sqrt{5x+9}\right)+2\left(x+2-\sqrt{3x+4}\right)=0\)
\(\Leftrightarrow x^2+x+\dfrac{3\left(x^2+x\right)}{x+3+\sqrt{5x+9}}+\dfrac{2\left(x^2+x\right)}{x+2+\sqrt{3x+4}}=0\)
\(\Leftrightarrow\left(x^2+x\right)\left(1+\dfrac{3}{x+3+\sqrt{5x+9}}+\dfrac{2}{x+2+\sqrt{3x+4}}\right)=0\)
\(\Leftrightarrow x^2+x=0\) (ngoặc phía sau luôn dương khi \(x\ge-\dfrac{4}{3}\))
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)