1/ cho tam giác ABC cân đỉnh A. đường cao BE;CF cắt nhau tại H. D là trung điểm của BC.
a/ chứng minh 4 điểm B;F;E;C cùng một đường tròn
b/ 4 điểmB;H;E;C có thuộc đường tròn không? vì sao?
c/ xác định tâm đường tròn đi qua 4 điểm A;F;B;C
d/ có thể khẳng định điểm B nằm ngoài đường tròn đi qua 4 điểm A;F;B;C không?
e/ chứng minh EF < BC
2/ cho ( O;R ); ( O';R') cắt nhau tại A;B (O;O' thuộc 2 nửa mặt phẳng bờ AB). trong cùng một nửa mặt phẳng bờ OO' vẽ hai bán kính OC; O'D sao cho OC//O'D. gọi E là điểm đối xứng của B qua OO'
a/ chứng minh AOBO' là hình thoi
b/ chứng minh AB;OO';CE đồng quy
c/ chứng minh A là trực tâm của tam giác BCD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

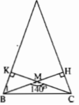
+) Xét tam giác vuông BKM có ∠BMC là góc ngoài tam giác tại đỉnh M nên:


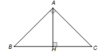
Do Tam giác ABC cân tại A, AH là đường cao nên H là trung điểm BC.
+Đáp án A. Ta có
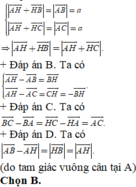

Đặt DH = x. Trên tia đối của tia DA em lấy điểm E sao cho DE = DH = x
=> tam giác BEH cân tại B => ^DBE = ^DBH (1) và BE = BH = 30
Mặt khác : ^ABD = ^ACD = ^BHD (2) ( góc có cạnh tương ứng vuông góc AC _|_ BH; CD _|_ DH)
(1) + (2) : ^ABD + ^DBE = ^BHD + ^DBH = 90o => tam giác ABE vuông tại B
Trong tg ABE vuông tại B đường cao BD nên ta có hệ thức:
DE.AE = BE²
<=> DE(AH + DH + DE) = BE²
<=> x(2x + 14) = 900
<=> 2x² + 14x - 900 = 0
Giải ra x = 18 ( loại nghiệm x = - 25)
=> AD = AH + DH = 14 + 18 = 32

a) Tam giác ABC cân tại A nên ABC = ACB (t/c tam giác cân)
=> ABC/2 = ACB/2
Mà ABD = CBD = ABC/2
ACE = BCE = ACB/2
Nên ABD = CBD = ACE = BCE
Xét t/g EBC và t/g DCB có:
góc EBC = DCB (cmt)
BC là cạnh chung
góc ECB = DBC (cmt)
Do đó, t/g EBC = t/g DCB (g.c.g)
=> BE = CD (2 cạnh tương ứng)
Mà AB = AC (gt) nên AB - BE = AC - CD
=> AE = AD
=> Tam giác AED cân tại A (đpcm)
b) tam giác ABC cân tại A => BAC = 180 độ - 2.ABC (1)
Tam giác EAD cân tại A => EAD = 180 độ - 2.AED (2)
Từ (1) và (2) => ABC = AED
Mà ABC và AED là 2 góc ở vị trí đồng vị nên ED // BC (đpcm)
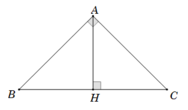

a)Nối F với D : E với D ta có:
Xét tam giác FBC ta có
D là trung điểm BC(1)
Góc BFC=90 (2)
Từ (1)(2)=>FD là trung tuyến của tam giác FBC
=>BD=CD=DF(*)
Chứng minh tương tự tam giác EBC
=>DE=DC=DB(**)
Từ (*)(**)=>BD=CD=DF=DE=(1/2BC)
=>B;F;E;C thuộc đừng tròn
=>D là tâm của đường tròn
B) Do B;H;E nằm trên cùng 1 đừng thẳng => H ko thuộc đừng tròn
=>B;H;E;c ko thuộc đừng tròn