Có 90 cách để chọn
6C4 X 4C2=90

6c4 và 4c2 bạn lấy ở đâucho mk cách giải đầy đủ đi rồi mk tick cho

Đáp án A

Có 2 trường hợp như sau

+)TH1: có 3 nam, 2 nữ, suy ra có cách chọn

+) TH2: có 4 nam, 1 nữ, suy ra có cách chọn

Suy ra xác suất cần tính bằng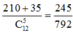 

Đáp án A

Có 2 trường hợp như sau

+)TH1: có 3 nam, 2 nữ, suy ra có C 5 3 C 7 2   =   210 cách chọn

+) TH2: có 4 nam, 1 nữ, suy ra có C 5 4 C 7 1   =   35 cách chọn

Suy ra xác suất cần tính bằng

so cach de lua chon ra 2 ban nam la3+2+1=6  cach. So cach de chon ra 2 ban Nữ la 5+4+3+2+1=15 cach. Sô cach de lua chon ra2 nam 2 Nữ la 15*6=90 cach

Có 90 cách để chọn
6C4 X 4C2=90

có 90 cách để chọn

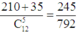
Chọn B.

Không gian mẫu có số phần tử là .

Gọi A là biến cố: “Trong 5 bạn được chọn có cả nam và nữ, đồng thời số nam nhiều hơn số nữ”. Khi đó, số kết quả thuận lợi cho biến cố A là: .

Vậy xác suất cần tính là .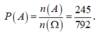

a) Có các TH:   

\(n=C^1_{25}\cdot C_{30}^9+C^2_{25}\cdot C_{30}^8+...+C_{25}^9\cdot C^1_{30}\)

b) Có ít nhất 1 nữ: (giống a)

c) Có nhiều nhất 2 nữ:

    + 2 nữ và 8 nam: \(C_{30}^2\cdot C_{25}^8\)

    + 1 nữ và 9 nam: \(C_{30}^1\cdot C_{25}^9\)

    + 0 nữ và 10 nam: \(C_{30}^0\cdot C_{25}^{10}\)

     \(\Rightarrow\) Cộng lại ta đc 535043135

Chọn ra 10 bạn bất kì: có \(C_{55}^{10}\) cách

Chọn 10 bạn ko có nữ nào: \(C_{25}^{10}\) cách

Chọn 10 bạn không có nam nào: \(C_{30}^{10}\) cách

a. Chọn 10 bạn có cả nam và nữ:

\(C_{55}^{10}-\left(C_{25}^{10}+C_{30}^{10}\right)\) cách

b. Có ít nhất 1 nữ:

\(C_{55}^{10}-C_{25}^{10}\) cách

c. Câu c làm như bạn trên

Chọn B

Số cách chọn một bạn nam và một bạn nữ để hát song ca là C 6 1 . C 4 1   =   24  

Số cách chọn là: 6 . 4 = 24  (cách).

Chọn: B