Biết x2+y2+z2+2x-4y+6z=-14. Tính x+y+z=???
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 4 2022
⇒(x−1)^2+4(y+1)^2+(z−3)^2≥0
x^2+4y^2+z^2-2x-6z+8y+15
=x^2+4y^2+z^2-2x-6z+8y+1+1+4+9
=(x^2-2x+1)+(4y^2+8y+4)+(z^2-6z+9)+1
=(x-1)^2+4(y+1)^2+(z-3^)2+1
Ta thấy:(x−1)^2≥0
4(y+1)^2≥0
(z−3)^ 2≥0
{(x−1)^24(y+1)^2(z−3)^2≥0
⇒(x−1)^2+4(y+1)^2+(z−3)^2≥0
⇒(x−1)2+4(y+1)2+(z−3)2+1≥0+1=1>0
CM
14 tháng 2 2018
Đáp án D.
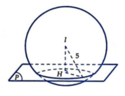
(P )//( α ) ⇒ ( P ) : 2 x − 2 y − z + c = 0 (c ≠ 14)
(S) có tâm I ( 1 ; 2 ; 3 ) , bán kính R=5
Hình tròn thiết diện (C) có S = 16 π =>Bán kính r = 4
Gọi H là hình chiếu của I lên (P) =>H là tâm của (C)
⇒ I H = d ( I ; ( P ) ) = R 2 − r 2 = 3
⇒ 2.1 − 2.2 − 3 + c 2 2 + 2 2 + 1 2 = 3 ⇔ c − 5 = 9 ⇔ c = 14 ( 1 ) c = − 4 ⇒ ( P ) : 2 x − 2 y − z − 4 = 0
27 tháng 9 2016
\(x^2+y^2+z^2+2x-4y+6z=-14\)
\(\Leftrightarrow\left(x^2+2x+1\right)+\left(y^2-4y+4\right)+\left(z^2+6z+9\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2+\left(y-2\right)^2+\left(z+3\right)^2=0\)
\(\Leftrightarrow\begin{cases}x+1=0\\y-2=0\\z+3=0\end{cases}\)\(\Leftrightarrow\begin{cases}x=-1\\y=2\\z=-3\end{cases}\)
\(\Rightarrow x+y+z=-1+2-3=-2\)
CM
30 tháng 1 2019
Chọn B.
Mặt cầu (S) tâm I(-1;2;3) và 
Do mặt phẳng (α)//(P) nên (α) có dạng : x + 2y - 2z + m = 0.
Do (α) tiếp xúc với (S) ⇔ d(I,(α)) = R.
* Với m = - 6 suy ra mặt phẳng có phương trình: x + 2y - 2z - 6 = 0.
* Với m = 12 suy ra mặt phẳng có phương trình: x + 2y - 2z + 12 = 0.
CM
30 tháng 10 2018
Chọn B.
Mặt cầu (S) tâm I(-1;2;3) và 
Do mặt phẳng (α)//(P) nên (α) có dạng : x + 2y - 2z + m = 0.
Do (α) tiếp xúc với (S) ⇔ d(I,(α)) = R.
* Với m = - 6 suy ra mặt phẳng có phương trình: x + 2y - 2z - 6 = 0.
* Với m = 12 suy ra mặt phẳng có phương trình: x + 2y - 2z + 12 = 0.