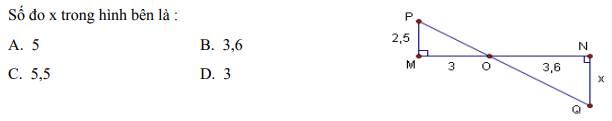 Giúp mik với mik cảm ưn :3
Giúp mik với mik cảm ưn :3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chiều từ cực dương đến cực âm
\(I=I_1=I_2=0,5A\\ U_2=U-U_1=3,5V\)
Đèn sẽ không sáng do hiệu điện thế trong mạch nhỏ hơn hiệu điện thế của 2 đèn
a)
b)vì các đèn mắc nối tiếp nên:
\(I=I_1=I_2=0,5A\)
vì các đèn mắc nối tiếp nên:
\(U=U_1+U_2\)
\(=>U_2=U-U_1=8-4,5=3,5\left(V\right)\)
c)nếu với một bóng đèn nhất định(có HĐT định mức), thì hiệu điện thế đặt vào hai đầu bóng đèn sẽ giảm dần ( tức là độ sáng của hai đèn yếu đi)

\(\dfrac{x+1}{199}+\dfrac{x+2}{198}+\dfrac{x+3}{197}+\dfrac{x+4}{196}+\dfrac{x+220}{5}=0\)
\(\Leftrightarrow\left(\dfrac{x+1}{199}+1\right)+\left(\dfrac{x+2}{198}+1\right)+\left(\dfrac{x+3}{197}+1\right)+\left(\dfrac{x+4}{196}+1\right)+\dfrac{x+200}{5}+\dfrac{20}{5}-4=0\)
\(\Leftrightarrow\dfrac{x+200}{199}+\dfrac{x+200}{198}+\dfrac{x+200}{197}+\dfrac{x+200}{196}+\dfrac{x+200}{5}=0\)
\(\Leftrightarrow\left(x+200\right)\left(\dfrac{1}{199}+\dfrac{1}{198}+\dfrac{1}{197}+\dfrac{1}{196}+\dfrac{1}{5}\right)=0\)
\(\Leftrightarrow x=-200\)( do \(\dfrac{1}{199}+\dfrac{1}{198}+\dfrac{1}{197}+\dfrac{1}{196}+\dfrac{1}{5}>0\))
\(\dfrac{x+1}{199}+\dfrac{x+2}{198}+\dfrac{x+3}{197}+\dfrac{x+4}{196}+\dfrac{x+220}{5}=0\\ \Leftrightarrow\left(\dfrac{x+1}{199}+1\right)+\left(\dfrac{x+2}{198}+1\right)+\left(\dfrac{x+3}{197}+1\right)+\left(\dfrac{x+4}{196}+1\right)+\left(\dfrac{x+220}{5}-4\right)=0\\ \Leftrightarrow\dfrac{x+200}{199}+\dfrac{x+200}{198}+\dfrac{x+200}{197}+\dfrac{x+200}{196}+\dfrac{x+200}{5}=0\\ \Leftrightarrow\left(x+200\right)\left(\dfrac{1}{199}+\dfrac{1}{198}+\dfrac{1}{197}+\dfrac{1}{196}+\dfrac{1}{5}\right)=0\\ \Leftrightarrow x=-200\)

uses crt;
var i,n:integer;
s:real;
begin
clrscr;
readln(n);
s:=0;
for i:=1 to n do
s:=s+(i/(i*sqr(i+5)));
writeln(s:4:2);
readln;
end.

ĐKXĐ : 2x \(\ge\)0 <=> x \(\ge\)0
| 7 + x | = 2x <=> \(\orbr{\begin{cases}7+x=2x\\7+x=-2x\end{cases}}\)
<=> \(\orbr{\begin{cases}x=7\\x=\frac{-7}{3}\end{cases}}\)( KTMĐK)
Vậy x = 7

\(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}\\xy=6\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}3x=2y\\xy-6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y=0\\xy-6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3xy-2y^2=0\\3xy-18=0\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}-2y^2-\left(-18\right)=0\\3xy-2y^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\9x-18=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\x=2\end{matrix}\right.\)

\(\frac{2}{a}-\frac{b+1}{3}=\frac{1}{2}\)
=> \(\frac{6-ab+a}{3a}=\frac{1}{2}\)
=> 2(6 - ab + a) = 3a
=> 12 - 2ab + 2a = 3a
=> 2ab + a = 12
=> a(2b + 1) = 12
Ta có 12 = 1.12 = (-1).(-12) = 3.4 = (-3).(-4) = 6.2 = (-6).(-2)
Lập bảng xét 12 trường hợp
| a | 1 | 12 | -1 | -12 | 4 | 3 | -4 | -3 | 6 | 2 | -2 | -6 |
| 2b + 1 | 12 | 1 | -12 | -1 | 3 | 4 | -3 | -4 | 2 | 6 | -6 | -2 |
| b | 5,5 | 0 | -6,5 | -1 | 1 | 1,5 | -2 | -2,5 | 0,5 | 2,5 | -3,5 | -1,5 |
Vậy các cặp (a;b) nguyên thỏa mãn là (12 ; 0) ;(-12 ; -1) ; (4 ; 1) ; (-4 ; -2)
Bg (phải thế này không ?)
\(\frac{2}{a}-\frac{b+1}{3}=\frac{1}{2}\)
\(\frac{2}{a}=\frac{1}{2}+\frac{b+1}{3}\)
\(\frac{2}{a}=\frac{3}{6}+\frac{2.\left(b+1\right)}{6}\)
\(\frac{2}{a}=\frac{3}{6}+\frac{2b+2}{6}\)
\(\frac{2}{a}=\frac{3+2b+2}{6}\)
\(\frac{2}{a}=\frac{2b+5}{6}\)
\(\frac{12}{a}=2b+5\)
\(a.\left(2b+5\right)=12\)= 1.12 = 12.1 = 3.4 = 4.3 = 2.6 = 6.2 = -1.(-12) = -12.(-1) = -3.(-4) = -4.(-3) = -2.(-6) = -6.(-2)
Nhận thấy 2b + 5 lẻ
=> a.(2b + 5) = 12.1 = 4.3 = -12.(-1) = -4.(-3)
Lập bảng:
| a = 12 | 2b + 5 = 1 | a = 4 | 2b + 5 = 3 | a = -12 | 2b + 5 = -1 | a = -4 | 2b + 5 = -3 |
| => b = -2 | => b = -1 | => b = -3 | => b = -4 |
Vậy các cặp {a; b} thỏa mãn là: (12; -2) ; (4; -1) ; (-12; -3) ; (-4; -4)

a) b)
x\(\begin{matrix}\text{3 phút 15 giây}\\6\\\overline{\text{19 phút 30 giây}}\end{matrix}\) +\(\begin{matrix}\text{9 giờ 25 phút}\\\text{5 giờ 45 phút}\\\overline{\text{15 giờ 10 phút }}\end{matrix}\)
c)
x\(\begin{matrix}235,05\\4,2\\\overline{987,21}\end{matrix}\)
d)
\(91,25\) \(25\)
\(75\) \(3,65\)
\(162\)
\(150\)
\(125\)
\(0\)
Ta có: \(\left\{{}\begin{matrix}MP\bot MN\\NQ\bot MN\end{matrix}\right.\left(gt\right)\)\(\Rightarrow MP//NQ\) (t/c)
Xét \(\Delta NOQ\) có: \(MP//NQ\) (cmt)
\(\Rightarrow\dfrac{NQ}{MP}=\dfrac{NO}{MO}\) (hệ quả đli Talét)
\(\Rightarrow\dfrac{x}{2,5}=\dfrac{3,6}{3}\Rightarrow x=3\)
\(\rightarrow\) Chọn D. 3