
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Xét tam giác AIB và tam giác CID có;
AI = CI ( vì I là trung điểm AC)
BI = DI ( vì I là trung điểm BD)
góc AIB = góc DIC ( cặp góc đối đỉnh )
=> tam giác AIB = tam giác CID ( c.g.c) (đpcm)
b. Xét tứ giác ABCD có: hai đường chéo AC và BD cắt nhau tại trung điểm I của mỗi đường => ABCD là hình bình hành
=> AD = BC và AD // BC (đpcm)
c.Do ABCD là hình bình hành (cmt)
=> AB // DC
=>góc DCA = góc BAC ( hai góc so le trong)
=> để CD vuông góc với AC thì góc DCA = 90o hay góc BAC = 90o hay tam giác ABC phải vuông tại A
Vậy điều kiện để CD vuông góc với AC là tam giác ABC phải vuông tại A
=))) Viết nhiều qué k cho mình nhe :333

a) Vì EFGH là tứ giác nên \(\widehat{E}+\widehat{F}+\widehat{G}+\widehat{H}=360^0\)
\(\Leftrightarrow6x-4+5x+14+5x-14+3x+22=360^0\)
\(\Leftrightarrow19x+18=360^0\)
\(\Leftrightarrow19x=342^0\)
\(\Leftrightarrow x=18\)
Thay x=18 vào các góc E;H;G;F ta được
\(\widehat{E}=104^0\); \(\widehat{H}=76^0\); \(\widehat{G}=76^0\); \(\widehat{F}=104^0\)
Vì \(\widehat{E}+\widehat{H}=104^0+76^0=180^0\)mà chúng ở vị trí trong cùng phía nên EF//GH mà \(\widehat{H}=\widehat{G}=76^0\)nên EFGH là hình thang cân
b) Vì EF//HI (I thuộc HG va EF//HG) và FI//EH suy ra EFIH la hình bình hành
suy ra EF=HI
Vì EFGH là htc nên EH=FG và EG=HF
Tự vẽ hình nha

Bài 3:
b: Xét ΔABC có
I là trung điểm của BC
IK//AC
Do đó: K là trung điểm của AB
Xét ΔABC có
I là trung điểm của BC
IH//AB
Do đó: H là trung điểm của AC
Xét ΔABC có
K là trung điểm của AB
H là trung điểm của AC
Do đó: HK là đường trung bình của ΔABC
Suy ra: HK//BC

a: Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
Suy ra: AH=DE
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
c: Xét ΔAHB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
hay AD/AC=AE/AB
Xét ΔADE vuông tại A và ΔACB vuông tại A có
AD/AC=AE/AB
Do đó: ΔADE\(\sim\)ΔACB

a: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)
b: \(=\dfrac{x^2-2x-3+x^2+2x-3+2x-2x^2}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x+3}\)
c: \(=\dfrac{6-7+x}{3\left(x-1\right)}=\dfrac{x-1}{3\left(x-1\right)}=\dfrac{1}{3}\)
d: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)

3h40p= \(\dfrac{11}{3}\) giờ
gọi thời gian đi là: x
thời gian về là: \(\dfrac{11}{3}\)-x
theo đề ta có:
50x=60(\(\dfrac{11}{3}\)-x)
<=> 50x= 220-60x
<=>50x+60x=220
<=>110x=220
<=>x=2
Quãng đường từ A -> B là:
50.2=100 (km)

a) Ta có: \(\left(2x+7\right)^2=\left(x+3\right)^2\)
\(\Leftrightarrow\left(2x+7\right)^2-\left(x+3\right)^2=0\)
\(\Leftrightarrow\left(2x+7-x-3\right)\left(2x+7+x+3\right)=0\)
\(\Leftrightarrow\left(x+4\right)\cdot\left(3x+10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\3x+10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\3x=-10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=-\dfrac{10}{3}\end{matrix}\right.\)
Vậy: \(S=\left\{-4;-\dfrac{10}{3}\right\}\)
b) Ta có: \(\left(4x+14\right)^2=\left(7x+2\right)^2\)
\(\Leftrightarrow\left(4x+14\right)^2-\left(7x+2\right)^2=0\)
\(\Leftrightarrow\left(4x+14-7x-2\right)\left(4x+14+7x+2\right)=0\)
\(\Leftrightarrow\left(-3x+12\right)\left(11x+16\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-3x+12=0\\11x+16=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-3x=-12\\11x=-16\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{16}{11}\end{matrix}\right.\)Vậy: \(S=\left\{4;-\dfrac{16}{11}\right\}\)
(2x+7)2=(x+3)2
=>(2x+7)2-(x+3)2=0
=>(2x+7-x-3)(2x+7+x+3)=0
=>(x-4)(3x+10)=0
=>x-4=0 hoặc 3x+10=0
TH1:x-4=0=>x=4
TH2:3x+10=0=>x=-10/3
(4x+14)2=(7x+2)2
(4x+14)2-(7x+2)2=0
(4x+14-7x-2)(4x+14+7x+2)=0
(-3x+12)(11x+16)=0
TH1:-3x+12=0=>x=4
TH2:11x+16=0=>x=-16/11
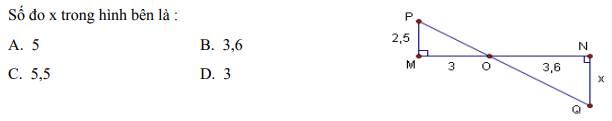 Giúp mik với mik cảm ưn :3
Giúp mik với mik cảm ưn :3



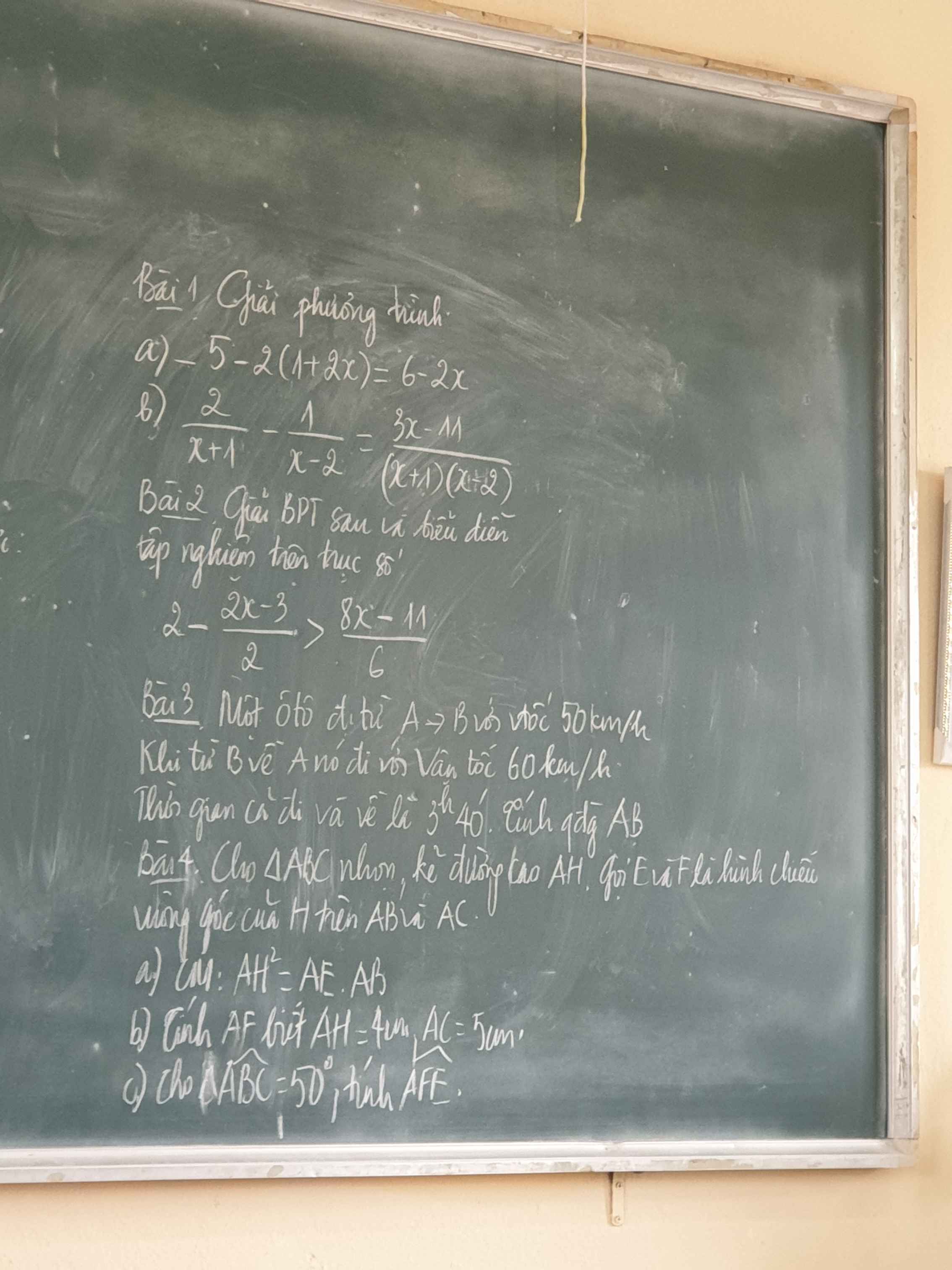
Ta có: \(\left\{{}\begin{matrix}MP\bot MN\\NQ\bot MN\end{matrix}\right.\left(gt\right)\)\(\Rightarrow MP//NQ\) (t/c)
Xét \(\Delta NOQ\) có: \(MP//NQ\) (cmt)
\(\Rightarrow\dfrac{NQ}{MP}=\dfrac{NO}{MO}\) (hệ quả đli Talét)
\(\Rightarrow\dfrac{x}{2,5}=\dfrac{3,6}{3}\Rightarrow x=3\)
\(\rightarrow\) Chọn D. 3