ai giúp em 2 bài 2 với ạ
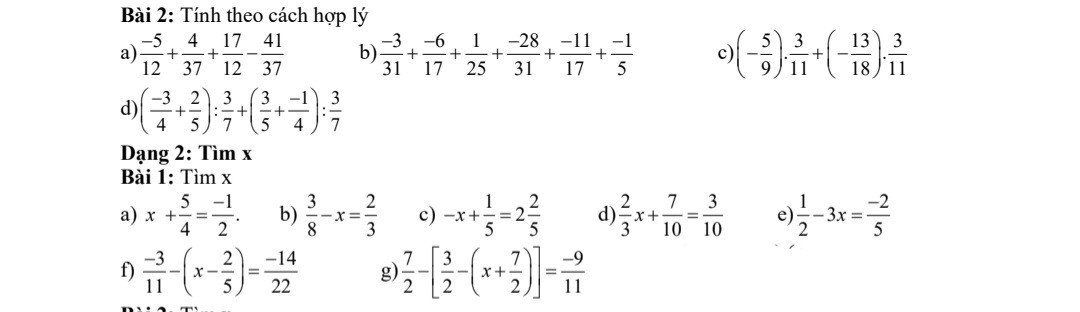
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a. $x^2=12y^2+1$ lẻ nên $x$ lẻ
Ta biết một scp khi chia 8 dư $0,1,4$. Mà $x$ lẻ nên $x^2$ chia $8$ dư $1$
$\Rightarrow 12y^2+1\equiv 1\pmod 8$
$\Rightarrow 12y^2\equiv 0\pmod 8$
$\Rightarrow y^2\equiv 0\pmod 2$
$\Rightarrow y$ chẵn. Mà $y$ nguyên tố nên $y=2$.
Khi đó: $x^2=12y^2+1=12.2^2+1=49\Rightarrow x=7$ (tm)
Bài 2:
b.
$x^2=8y+1$ nên $x$ lẻ. Đặt $x=2k+1$ với $k$ tự nhiên.
Khi đó: $8y+1=x^2=(2k+1)^2=4k^2+4k+1$
$\Rightarrow 2y=k(k+1)$
Vì $(k,k+1)=1, k< k+1$ và $y$ nguyên tố nên xảy ra các TH sau:
TH1: $k=2, k+1=y\Rightarrow y=3\Rightarrow x=5$ (tm)
TH2: $k=1, k+1=2y\Rightarrow y=1$ (vô lý)
TH3: $k=y, k+1=2\Rightarrow y=1$ (vô lý)
Vậy $(x,y)=(5,3)$ là đáp án duy nhất thỏa mãn.

Bài 15:
\(P=\dfrac{x+y-1}{x\left(x+y\right)}+\dfrac{x-y}{2xy}\cdot\dfrac{xy+y^2+xy-y^2}{x\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{1}{x}\)

Bài 3:
Số học sinh kém là:
40-8-10-20=2(bạn)
Tỉ số phần trăm giữa số học sinh giỏi so với lớp là:
8:40=20%
Tỉ số phần trăm giữa số học sinh khá so với lớp là:
20:40=50%
Tỉ số phần trăm giữa số học sinh trung bình so với lớp là:
10:40=25%
Tỉ số phần trăm giữa số học sinh yếu so với lớp là:
2:40=5%

Bài 2:
a: \(Q=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{5}\)
\(=\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{5}{\sqrt{x}-1}\)
\(=\dfrac{x+2+\sqrt{x}\left(\sqrt{x}-1\right)-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{5}{\sqrt{x}-1}\)
\(=\dfrac{-\sqrt{x}+1+x-\sqrt{x}}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{5}{x+\sqrt{x}+1}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{5}{x+\sqrt{x}+1}=\dfrac{5}{x+\sqrt{x}+1}\)
b: Khi x=4-2căn 3 thì \(Q=\dfrac{5}{4-2\sqrt{3}+\sqrt{4-2\sqrt{3}}+1}\)
\(=\dfrac{5}{5-2\sqrt{3}+\sqrt{3}-1}=\dfrac{5}{4-\sqrt{3}}=\dfrac{20+5\sqrt{3}}{13}\)
c: \(x+\sqrt{x}+1=\sqrt{x}\left(\sqrt{x}+1\right)+1>=1>0\forall x\) thỏa mãn ĐKXĐ
5>0
Do đó: \(Q=\dfrac{5}{x+\sqrt{x}+1}>0\forall x\) thỏa mãn ĐKXĐ
d: \(Q\cdot\left(\dfrac{x+\sqrt{x}+1}{\sqrt{x}+1}\right)< 1\)
=>\(\dfrac{5}{x+\sqrt{x}+1}\cdot\dfrac{x+\sqrt{x}+1}{\sqrt{x}+1}< 1\)
=>\(\dfrac{5}{\sqrt{x}+1}< 1\)
=>\(\dfrac{5-\sqrt{x}-1}{\sqrt{x}+1}< 0\)
=>\(4-\sqrt{x}< 0\)
=>\(\sqrt{x}>4\)
=>x>16

Câu 1:
Ta có: \(\left(3x+7\right)\left(2x+3\right)-\left(3x-5\right)\left(2x+11\right)\)
\(=6x^2+9x+14x+21-\left(6x^2+33x-10x-55\right)\)
\(=6x^2+23x+21-6x^2-23x+55\)
=76

2:
a: =>1/3x=16+1/4-13-1/4=3
=>x=9
b: =>4,5-2x=11/14:(-11/7)=-1/2=-0,5
=>2x=5
=>x=2,5
3:
Số học sinh giỏi là 12*5/6=10 bạn
Số học sinh trung bình là 10*1,4=14 bạn
Số học sinh của lớp là 10+12+14=36 bạn


Bài IV:
1: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
2: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của BA
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(3\right)\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD tại C
=>AC\(\perp\)DM tại C
Xét ΔADM vuông tại A có AC là đường cao
nên \(MC\cdot MD=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MA^2=MH\cdot MO=MC\cdot MD\)
3: Ta có: \(\widehat{MAI}+\widehat{OAI}=\widehat{OAM}=90^0\)
\(\widehat{HAI}+\widehat{OIA}=90^0\)(ΔAHI vuông tại H)
mà \(\widehat{OAI}=\widehat{OIA}\)
nên \(\widehat{MAI}=\widehat{HAI}\)
=>AI là phân giác của góc HAM
Xét ΔAHM có AI là phân giác
nên \(\dfrac{HI}{IM}=\dfrac{AH}{AM}\left(5\right)\)
Xét ΔOHA vuông tại H và ΔOAM vuông tại A có
\(\widehat{HOA}\) chung
Do đó: ΔOHA đồng dạng với ΔOAM
=>\(\dfrac{OH}{OA}=\dfrac{HA}{AM}\)
=>\(\dfrac{OH}{OI}=\dfrac{AH}{AM}\left(6\right)\)
Từ (5) và (6) suy ra \(\dfrac{OH}{OI}=\dfrac{IH}{IM}\)
=>\(HO\cdot IM=IO\cdot IH\)
Bài 2:
a)
\(\dfrac{-5}{12}+\dfrac{4}{37}+\dfrac{17}{12}-\dfrac{41}{37}\\ =\left(-\dfrac{5}{12}+\dfrac{17}{12}\right)+\left(\dfrac{4}{37}-\dfrac{41}{37}\right)\\ =\left(-1\right)+\left(-1\right)\\ =-2\)
b)
\(-\dfrac{3}{31}+\dfrac{-6}{17}+\dfrac{1}{25}+\dfrac{-28}{31}+\dfrac{-11}{17}+\dfrac{-1}{5}\\ =\left(\dfrac{-3}{31}-\dfrac{28}{31}\right)+\left(\dfrac{-6}{17}-\dfrac{11}{17}\right)+\left(\dfrac{1}{25}-\dfrac{1}{5}\right)\\ =\left(-1\right)+\left(-1\right)+\dfrac{-4}{25}\\ =-\dfrac{4}{25}-2\\ =-\dfrac{52}{25}\)
c)
\(\left(\dfrac{-5}{9}\right)\cdot\dfrac{3}{11}+\left(\dfrac{-13}{18}\right)\cdot\dfrac{3}{11}\\ =\dfrac{3}{11}\cdot\left(\dfrac{-5}{9}+\dfrac{-13}{18}\right)\\ =\dfrac{3}{11}\cdot\left(\dfrac{-10}{18}+\dfrac{-13}{18}\right)\\ =\dfrac{3}{11}\cdot\dfrac{-23}{18}\\ =\dfrac{-23}{66}\)
d)
\(\left(\dfrac{-3}{4}+\dfrac{2}{5}\right):\dfrac{3}{7}+\left(\dfrac{3}{5}+\dfrac{-1}{4}\right):\dfrac{3}{7}\\ =\left(\dfrac{-3}{4}+\dfrac{2}{5}\right)\cdot\dfrac{7}{3}+\left(\dfrac{3}{5}-\dfrac{1}{4}\right)\cdot\dfrac{7}{3}\\ =\dfrac{7}{3}\cdot\left(\dfrac{-3}{4}+\dfrac{2}{5}+\dfrac{3}{5}-\dfrac{1}{4}\right)\\ =\dfrac{7}{3}\cdot\left(-1+1\right)\\ =\dfrac{7}{3}\cdot0\\ =0\)