nhờ các bạn giải giúp mk câu d là được

a.\(m=1\)

\(\Leftrightarrow x^2-2.1x+1^2-1-3=0\)

\(\Leftrightarrow x^2-2x-3=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\) ( Vi-ét )

b.\(\Delta=\left(-2m\right)^2-4\left(m^2-m-3\right)\)

      \(=4m^2-4m^2+4m+12\)

      \(=4m+12\)

Để pt có nghiệm kép thì \(\Delta=0\)

                                        \(\Leftrightarrow4m+12=0\) 

                                         \(\Leftrightarrow m=-3\)

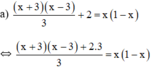
⇔ (x + 3)(x – 3) + 2.3 = 3x(1 – x)

⇔ x 2 − 9 + 6 = 3 x − 3 x 2 ⇔ x 2 − 9 + 6 − 3 x + 3 x 2 = 0 ⇔ 4 x 2 − 3 x − 3 = 0

Có a = 4; b = -3; c = -3  ⇒   Δ   =   ( - 3 ) 2   –   4 . 4 . ( - 3 )   =   57   >   0

Phương trình có hai nghiệm

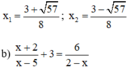
Điều kiện xác định: x ≠ 5; x ≠ 2.

Quy đồng và khử mẫu ta được :

(x + 2)(2 – x) + 3(2 – x)(x – 5) = 6(x – 5)

⇔ 4 − x 2 + 6 x − 3 x 2 − 30 + 15 x = 6 x − 30 ⇔ 4 − x 2 + 6 x − 3 x 2 − 30 + 15 x − 6 x + 30 = 0 ⇔ − 4 x 2 + 15 x + 4 = 0

Có a = -4; b = 15; c = 4  ⇒   Δ   =   15 2   –   4 . ( - 4 ) . 4   =   289   >   0

Phương trình có hai nghiệm phân biệt:

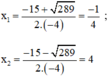
Cả hai giá trị đều thỏa mãn điều kiện.

Vậy phương trình có tập nghiệm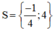 

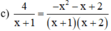
Điều kiện xác định: x ≠ -1; x ≠ -2.

Quy đồng và khử mẫu ta được:

4 ⋅ ( x + 2 ) = − x 2 − x + 2 ⇔ 4 x + 8 = − x 2 − x + 2 ⇔ 4 x + 8 + x 2 + x − 2 = 0 ⇔ x 2 + 5 x + 6 = 0

Có a = 1; b = 5; c = 6  ⇒   Δ   =   5 2   –   4 . 1 . 6   =   1   >   0

⇒ Phương trình có hai nghiệm phân biệt:

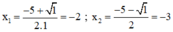
Chỉ có nghiệm x 2   =   - 3  thỏa mãn điều kiện xác định.

Vậy phương trình có nghiệm x = -3.

\(\hept{\begin{cases}3x-2y=1\\mx+3y=4\end{cases}}\)

\(\hept{\begin{cases}3x=1+2y\\mx+3y=4\end{cases}}\)

\(\hept{\begin{cases}x=1+\frac{2y}{3}\\mx+3y=4\end{cases}}\)

a, Khi thay m = 1 thì biểu thức mx + 3y ta đc

\(x+3y=4\)

Hệ phương trình trở thành : \(\hept{\begin{cases}x=1+\frac{2y}{3}\\x+3y=4\end{cases}}\)

Ta thay x vào biểu thức x + 3y = 4 ta đc

\(1+\frac{2y}{3}+3y=4\)

\(1+\frac{2y}{3}+\frac{9y}{3}-4=0\)

\(-3+\frac{11y}{3}=0\)

\(\frac{11y}{3}=3\Leftrightarrow11y=9\Leftrightarrow y=\frac{9}{11}\)

Ta thay y = 9/11 vào biểu thức x + 3y ta đc

\(x+3.\frac{9}{11}=4\)

\(x+\frac{27}{11}=4\)

\(x=\frac{17}{11}\)

Vậy \(\left\{x;y\right\}=\left\{\frac{17}{11};\frac{9}{11}\right\}\)

a) thay m = 3 ta có pt:

x² + 10x + 3 = 0 

<=> xét delta phẩy 

25 - 3 = 22 

\(\left[{}\begin{matrix}x1=-5+\sqrt{22}\\x2=-5-\sqrt{22}\end{matrix}\right.\)

vậy S={ \(-5+\sqrt{22}\);\(-5-\sqrt{22}\)}

b) xét delta phẩy 

(m+2)² - m² + 6

= 4m +10 

để phương trình có 2 nghiệm x1;x2 thì delta phẩy ≥ 0 

=> m ≥ \(\dfrac{-10}{4}\)

theo Vi-ét ta có:

\(\left\{{}\begin{matrix}x1+x2=-2m-4\\x1x2=m^2-6\end{matrix}\right.\)

theo bài ra ta có:

x1² + x2² = 16

<=> (x1+x2)² - 2x1x2 = 16

=> 4m² + 16m + 16 - 2m² + 12 = 16

<=> 2m² + 16m + 12 = 0 

<=> m² + 8m + 6 = 0 

giải ra \(\left[{}\begin{matrix}m=-4+\sqrt{10}\\m=-4-\sqrt{10}\end{matrix}\right.\)

vậy m = \(-4+\sqrt{10}\) để pt có 2 nghiệm thỏa mãn hệ thức x1² + x2² = 16

( m = -4-\(\sqrt{10}\) loại)

a: Khi m=1 thì pt sẽ là: x+x-3=6x-6

=>6x-6=2x-3

=>4x=3

=>x=3/4

b: m^2x+m(x-3)=6(x-1)

=>x(m^2+m-6)=-6+3m=3m-6

=>x(m+3)(m-2)=3(m-2)

Để (1) có nghiệm duy nhất thì (m+3)(m-2)<>0

=>m<>-3 và m<>2

=>x=3/(m+3)

\(A=\dfrac{\left(\dfrac{3}{m+3}\right)^2+\dfrac{6}{m+3}+3}{\left(\dfrac{3}{m+3}\right)^2+2}\)

\(=\dfrac{9+6m+18+3m^2+18m+27}{\left(m+3\right)^2}:\dfrac{9+2m^2+12m+18}{\left(m+3\right)^2}\)

\(=\dfrac{3m^2+24m+54}{2m^2+12m+27}>=\dfrac{1}{2}\)

Dấu = xảy ra khi 6m^2+48m+108=2m^2+12m+27

=>4m^2+36m+81=0

=>m=-9/2

a) khi m = 1 ta có pt
x + 1.(x-3) = 6.(x-1) 
=> x + x - 3 = 6x - 6
=> -4x = -3
=> x = 3/4
vậy với m=1 pt có no x =3/4