[6.(-1/3)^3 -3.(-1/3)+1]:(-1/3-1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2}{5}\\x_1x_2=-\dfrac{7}{5}\end{matrix}\right.\)
b.
\(A=x_1^2+x_2^2-x_1x_2=\left(x_1+x_2\right)^2-3x_1x_2\)
\(=\left(\dfrac{2}{5}\right)^2-3\left(-\dfrac{7}{5}\right)=\dfrac{109}{25}\)

a: Khi m=2 thì pt sẽ là x^2-6x-3=0
=>\(x=3\pm2\sqrt{3}\)

`1)` Ptr có: `\Delta=3^2-4.5.(-1)=29 > 0 =>`Ptr có `2` nghiệm phân biệt
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=-3/5),(x_1.x_2=c/a=-1/5):}`
Có: `A=(3x_1+2x_2)(3x_2+x_1)`
`A=9x_1x_2+3x_1 ^2+6x_2 ^2+2x_1x_2`
`A=8x_1x_2+3(x_1+x_2)^2=8.(-1/5)+3.(-3/5)^2=-13/25`
Vậy `A=-13/25`
____________________________________________________
`2)` Ptr có: `\Delta'=(-1)^2-7.(-3)=22 > 0=>` Ptr có `2` nghiệm pb
`=>` Áp dụng Viét có: `{(x_1+x_2=[-b]/a=2/7),(x_1.x_2=c/a=-3/7):}`
Có: `M=[7x_1 ^2-2x_1]/3+3/[7x_2 ^2-2x_2]`
`M=[(7x_1 ^2-2x_1)(7x_2 ^2-2x_2)+9]/[3(7x_2 ^2-2x_2)]`
`M=[49(x_1x_2)^2-14x_1 ^2 x_2-14x_1 x_2 ^2+4x_1x_2+9]/[3(7x_2 ^2-2x_2)]`
`M=[49.(-3/7)^2-14.(-3/7)(2/7)+4.(-3/7)+9]/[3x_2(7x_2-2)]`
`M=6/[x_2(7x_2-2)]` `(1)`
Có: `x_1+x_2=2/7=>x_1=2/7-x_2`
Thay vào `x_1.x_2=-3/7 =>(2/7-x_2)x_2=-3/7`
`<=>-x_2 ^2+2/7 x_2+3/7=0<=>x_2=[1+-\sqrt{22}]/7`
`@x_2=[1+\sqrt{22}]/7=>M=6/[[1+\sqrt{22}]/7(7 .[1+\sqrt{22}]/2-2)]=2`
`@x_2=[1-\sqrt{22}]/7=>M=6/[[1-\sqrt{22}]/7(7 .[1-\sqrt{22}]/2-2)]=2`
Vậy `M=2`

Phương trình 2 x 2 − 11x + 3 = 0 3 = 97 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − b a x 1 . x 2 = c a ⇔ x 1 + x 2 = 11 2 x 1 . x 2 = 3 2
Ta có
A = x 1 2 + x 2 2 = x 1 + x 2 2 - 2 x 1 x 2 1 + x 2 ) = 11 2 2 − 2. 3 2 = 109 4
Đáp án: A

Đáp án B
Phương trình x 2 - 5 x + 2 = 0 có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có:
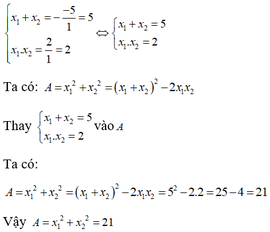

Phương trình 2 x 2 − 18x + 15 = 0 có = 61 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có
Ta có
( x 1 + x 2 ) 3 = x 1 3 + 3 x 12 x 2 + 3 x 1 x 22 + x 2 3 ⇒ ( x 1 + x 2 ) 3 = x 1 3 + x 2 3 + 3 x 1 x 2 ( x 1 + x 2 ) ⇒ x 1 3 + x 2 3 = ( x 1 + x 2 ) 3 − 3 x 1 x 2 ( x 1 + x 2 )
Nên
C = x 1 3 + x 2 3 = x 1 + x 2 3 - 3 x 1 x 2 ( x 1 + x 2 )
= 9 3 – 3 . 3 . 15 2 = 1053 2
Đáp án: B

Phương trình x 2 − 20x − 17 = 0 có = 468 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − b a x 1 . x 2 = c a ⇔ x 1 + x 2 = 20 x 1 . x 2 = − 17
Ta có
C = x 1 3 + x 2 3 = x 1 3 + 3 x 1 2 x 2 + 3 x 1 x 2 2 + x 2 3 − 3 x 1 2 x 2 − 3 x 1 x 2 2 = ( x 1 + x 2 ) 3 − 3 x 1 x 2 ( x 1 + x 2 ) = 2 3 – 3 . ( − 17 ) . 20 = 9020
Đáp án: D

Phương trình x 2 − 5x + 2 = 0 có = ( − 5 ) 2 – 4.1.2 = 17 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − b a x 1 . x 2 = c a ⇔ x 1 + x 2 = 5 x 1 . x 2 = 2
Ta có
A = x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 – 2 x 1 . x 2 = 5 2 – 2 . 2 = 21
Đáp án: B

Đáp án B
Phương trình x 2 - 5 x + 2 = 0 có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có:
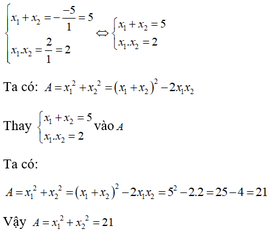

`[6.(-1/3)^3 -3.(-1/3)+1]:(-1/3-1)`
`= [6.((-1)^3)/(3^3)-(-3/3)+1]:(-1/3-3/3)`
`= [6. (-1/27) + 1+1]:(-4/3)`
`= [(-6/27) + (1+1)] . (-3/4)`
`= [-2/9 + 2] . (-3/4)`
`= [-2/9 + 18/9] . (-3/4)`
`= 16/9 . (-3/4)`
`= -4/3`
\(\left[6\left(-\dfrac{1}{3}\right)^3-3\cdot\left(-\dfrac{1}{3}\right)+1\right]:\left(-\dfrac{1}{3}-1\right)\)
\(=\left[6\cdot\dfrac{-1}{27}+1+1\right]:\dfrac{-4}{3}\)
\(=\left(-\dfrac{2}{9}+2\right):\dfrac{-4}{3}=\dfrac{16}{9}\cdot\dfrac{3}{-4}=\dfrac{-48}{36}=-\dfrac{4}{3}\)