a: Vì góc AKI=90 độ

nên K nằm trên đường tròn đường kính AI

b: Gọi G là trung điểm của AK

góc GKH=góc GKI+góc HKI

=góc GIK+góc HBI

=góc BIH+góc HBI=90 độ

=>HK là tiếp tuyến của (G)

Tham khảo
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB 
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG

b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
 góc IAG = góc KAG (cmt)
  AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)

c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có:  t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC

refer
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB 
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG

b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
 góc IAG = góc KAG (cmt)
  AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)

c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có:  t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC

a: Vì góc AKI=90 độ

nên K nằm trên đường tròn đường kính AI

b: Gọi G là trung điểm của AK

góc GKH=góc GKI+góc HKI

=góc GIK+góc HBI

=góc BIH+góc HBI=90 độ

=>HK là tiếp tuyến của (G)

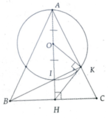
a, Chứng minh được  B K A ^ = 90 0

b, Gọi O là trung điểm AI

Ta có:

+ OK = OA =>  O K A ^ = O A K ^

+  O A K ^ = H B K ^ (cùng phụ  A C B ^ )

+ HB = HK =>  H B K ^ = H K B ^

=> O K A ^ = H K B ^ ⇒ H K O ^ = 90 0

Đáp án A

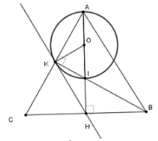
Gọi O là trung điểm AI. Xét tam giác vuông AIK có

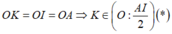
Xét tam giác OKA cân tại O (vì OA=OK=R) có:

O K A ^ = O A K ^  (1)

Xét tam giác CKB vuông tại K (vì  K B ⊥ A C ) có:

H là trung điểm CB (vì tam giác ABC cân tại A có AH là đường cao nên đồng thời là đường trung tuyến)

⇒ KH là trung tuyến ứng với cạnh huyền BC

⇒ H K C ^ = H C K ^   ( 2 )

Từ (1) và (2) suy ra  O K A ^ + H K C ^ = O A K ^ + H C K ^ = 90 o (vì  A H ⊥ B C )

Mà  O K A ^ + H K C ^ + O K H ^ = 180 o ⇒ O K H ^ = 90 o ⇒ O K ⊥ K H (**)

Từ (*) và (**) suy ra HK là tiếp tuyến của (O)

Chọn đáp án A

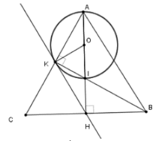
Gọi O là trung điểm AI. Xét tam giác vuông AIK có

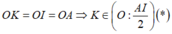
Từ (*) và (**) thì HK là tiếp tuyến của đường tròn đường kính AI

a: Ta có: ΔBKC vuông tại K

mà KH là trung tuyến

nên KH=BH

=>ΔHBK cân tại H

b: góc BAH=90 độ-góc ABC

góc IAK=90 độ-góc ACB

mà góc ABC=góc ACB

nên góc BAH=góc IAK

c: Gọi G là trung điểm của AI

góc GKH=góc GKI+góc HKI

=góc GIK+góc HBI

=góc BIH+góc HBI=90 độ

=>HK là tiếp tuyến của (G)

???, bạn ơi, hình như có 2 điểm M, : " AM cắt BC,BK lần  lượt tại M và N " ?

a: Vì góc AKB=góc AHB=90 độ

=>AKHB nội tiếp

b: góc FBC=góc HAC=góc EBC

=>BH là phân giác của góc EBI

còn song song dou ạ vẽ cho e cái hình dc hong e ngu toán í:(