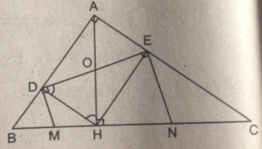
cho tam giác ABC cân tại A, đường cao BH, M thuộc BC. gọi D và E thứ tự là hình chiếu của M trên AB và AC. chứng minh rằng: MD+ME=BH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 8 2021
a) Xét tứ giác ADME có
AD//ME
DM//AE
Do đó: ADME là hình bình hành
b) Xét ΔEMC có \(\widehat{EMC}=\widehat{C}\left(=\widehat{B}\right)\)
nên ΔEMC cân tại E
Suy ra: EM=EC
Ta có: AE+EC=AC(E nằm giữa A và C)
mà AE=DM(AEMD là hình bình hành
mà EM=EC(cmt)
nên AC=MD+ME
2 tháng 10 2021
cho mình hỏi ngu tí là ở câu b đó ạ,từ đâu mà suy ra được góc EMC = C(=B) ạ :((
B1
30 tháng 7 2017
1 phần thôi nhé
Nối BE, Gọi P là giao điểm của AD với BE.
Áp dụng định lí Ceva cho tam giác ABE => AH/HE=BP/PE=> HP//AB(1).
Từ (1)=> Tam giác AHP cân tại H=> AH=HP.(2)
Ta cần chứng minh AD//CE <=> DP//CE <=> BD/BC=BP/BE <=> BD/BC=1-(EP/BE).(3)
Mà EP/BE=HP/AB (do (1))=> EP/BE= AH/AB=HD/DB (do (2) và tc phân giác). (4)
Khi đó (3)<=> BD/BC=1-(HD/DB) hay (BD/BC)+(HD/DB)=1 <=> BD^2+HD*BC=BC*DB
<=> BD^2+HD*BC= (BD+DC)*BD <=> BD^2+HD*BC= BD^2+BD*DC <=> HD*BC=BD*DC
<=> HD/DB=CD/BC <=> AH/AB=CD/BC. (5)
Chú ý: Ta cm được: CA=CD (biến đổi góc).
Nên (5) <=> AH/AB=CA/BC <=> Tg AHB đồng dạng Tg CAB.( luôn đúng)
=> DpCm.
CM
8 tháng 10 2019
Vì ADHE là hình chữ nhật nên OD = OH
Suy ra, tam giác ODH cân tại O ⇒ ∠ ODH = ∠ OHD
Mà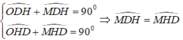 
Xét tam giác MBD có:
∠ (MDB) = ∠ (MBD) (vì cùng phụ với hai góc bằng nhau ∠ (MDH) = ∠ (MHD))
Suy ra, tam giác MBD cân tại M, do đó MD = MB (2)
Từ (1) và (2) suy ra, MB = MH
Vậy M là trung điểm của BH
Tương tự, ta cũng có N là trung điểm của CH.