Từ 1 điểm A cố định bên ngoài đường tròn (O), kẻ 1 tiếp tuyến AB và 1 cát tuyến ACD của đường tròn
a) Chứng minh ta luôn có \(^{AB^2=AC.AD}\)khi cát tuyến ACD thay đổi
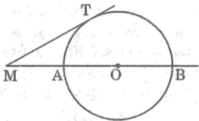
b) Tính bán kính của đường tròn biết cát tuyến ACD đi qua tâm của đường tròn và AB=30cm; AD=60cm

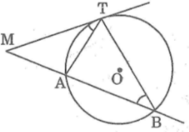

a, Ta có : góc ABC = góc CDB ( = 1/2 sđ cung BC nhỏ )
=> tam giác ABC đồng dạng với tam giác ADB (g.g)
=> AB/AD = AC/AB
=> AB^2 = AC.AD
Tk mk nha