
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Tương tự: \(\left\{{}\begin{matrix}SA\perp CD\\AD\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp SD\)
\(\left\{{}\begin{matrix}SA\perp BD\\AC\perp BD\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow\left(SBD\right)\perp\left(SAC\right)\)
b.
Do M, N là trung điểm SB, SD \(\Rightarrow\) MN là đường trung bình tam giác SBD
\(\Rightarrow MN||BD\)
Mà \(BD\perp\left(SAC\right)\) (cmt) \(\Rightarrow MN\perp\left(SAC\right)\)
c.
K là trung điểm SA, M là trung điểm SB \(\Rightarrow KM\) là đường trung bình tam giác SAB
\(\Rightarrow KM||AB\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\Rightarrow SA\perp KM\) (1)
Hoàn toàn tương tự ta có \(SA\perp KN\) (2)
(1); (2) \(\Rightarrow SA\perp\left(KMN\right)\)
d.
Từ A kẻ \(AH\perp SO\)
Do \(BD\perp\left(SAC\right)\) (cmt) \(\Rightarrow BD\perp AH\)
\(\Rightarrow AH\perp\left(SBD\right)\)
\(\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
\(SA=\sqrt{SB^2-AB^2}=2a\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{a\sqrt{2}}{2}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AO^2}\Rightarrow AH=\dfrac{SA.OA}{\sqrt{SA^2+OA^2}}=\dfrac{2a}{3}\)

![]()
![]()
![]()
![]()
![]()
và do đó phương trình đã cho tương đương với
![]()
![]()
Vậy đáp án là D.

Hàm số y 1 = sin π 2 − x có chu kì T 1 = 2 π − 1 = 2 π
Hàm số y 2 = cot x 3 có chu kì T 2 = π 1 3 = 3 π
Suy ra hàm số đã cho y = y 1 + y 2 có chu kì T = B C N N 2 , 3 π = 6 π .
Vậy đáp án là D.

Mỗi lần cắt một mảnh giấy thành 7 mảnh, tức là Mạnh tạo thêm 6 mảnh giấy. Do đó công thức tính số mảnh giấy theo n bước được thực hiện là Sn = 6n + 1. Ta chứng minh tính đúng đắn của công thức trên bằng phương pháp quy nạp theo n.
Bước cơ sở. Mạnh cắt mảnh giấy thành 7 mảnh, n =1, S(1) = 6.1+1 =7
Công thức đúng với n = 1
Bước quy nạp: giả sử sau k bước, Mạnh nhận được số mảnh giấy là S(k) = 6k + 1
Sang bước thứ k +1, Mạnh lấy một trong số những mảnh giấy nhận được trong k bước trước và cắt thành 7 mảnh. Tức là Mạnh đã lấy đi 1 trong S(k) mảnh và thay vào đó 7 mảnh được cắt ra. Vậy tổng số mảnh giấy ở bước k + 1 là: S(k =1) = S(k) -1 + 7= S(k) + 6 = 6k + 1 + 1 = 6(k+1) +1
Vậy công thức S(n) đúng với mọi n ∈N* . Theo công thức trên chỉ có phương án D thoả mãn vì 121 =6.20 + 1
Đáp án D



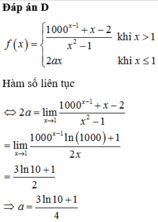
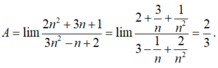
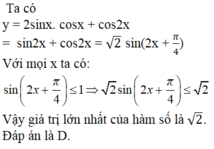
a/
\(SH\perp\left(ABCD\right);CD\in\left(ABCD\right)\Rightarrow CD\perp SH\)
ABCD là HCN \(\Rightarrow CD\perp AD\)
\(\Rightarrow CD\perp\left(SAD\right)\)
\(\Rightarrow\widehat{CSD}\) là góc giữa SC với (SAD)
Ta có
\(SH\perp\left(ABCD\right);AD\in\left(ABCD\right)\Rightarrow SH\perp AD\)
Xét tg vuông SHD có
\(SD=\sqrt{SH^2+HD^2}\) Mà HD=AD-AH=3a-a=2a
\(\Rightarrow SD=\sqrt{8a^2+4a^2}=2a\sqrt{3}\)
Ta có
\(CD\perp\left(SAD\right);SD\in\left(SAD\right)\Rightarrow CD\perp SD\)
Xét tg vuông SCD có
\(\tan\widehat{CSD}=\dfrac{CD}{SD}=\dfrac{2a}{2a\sqrt{3}}=\dfrac{\sqrt{3}}{3}\Rightarrow\widehat{CSD}=30^o\)
b/
Ta có
\(SH\perp\left(ABCD\right);SH\in\left(SHB\right)\Rightarrow\left(SHB\right)\perp\left(ABCD\right)\)
\(SH\perp\left(ABCD\right);SH\in\left(SHI\right)\Rightarrow\left(SHI\right)\perp\left(ABCD\right)\)
Xét tg vuông ABH có
\(BH^2=AB^2+AH^2=4a^2+a^2=5a^2\)
Xét tg vuông DHI có
\(HI^2=HD^2+DI^2=4a^2+a^2=5a^2\)
Xét tg vuông BCI có
\(BI^2=BC^2+CI^2=9a^2+a^2=10a^2\)
Xét tg BHI có
\(BI^2=BH^2+HI^2=5a^2+5a^2=10a^2\)
=> tg BHI là tg vuông cân tại H
Ta có
\(SH\perp\left(ABCD\right);HI\in\left(ABCD\right)\Rightarrow HI\perp SH\)
\(HI\perp HB\left(cmt\right)\)
\(\Rightarrow HI\perp\left(SHB\right);HI\in\left(SHI\right)\Rightarrow\left(SHI\right)\perp\left(SHB\right)\)
c/
Ta có
\(SH\perp\left(ABCD\right);BH\in\left(ABCD\right)\Rightarrow SH\perp HB\)
\(SH\perp\left(ABCD\right);HI\in\left(ABCD\right)\Rightarrow SH\perp HI\)
Xét tg vuông SHB có
\(SB=\sqrt{SH^2+BH^2}=\sqrt{8a^2+5a^2}=a\sqrt{13}\)
Xét tg vuông SHI có
\(SI=\sqrt{SH^2+HI^2}=\sqrt{8a^2+5a^2}=a\sqrt{13}\)
=> SB=SI => tg SBI cân tại S
Gọi K là trung điểm BI => \(SK\perp BI\) (trong tg cân đường trung tuyến xuất phát từ đỉnh tg cân đồng thời là đường cao)
c/m tương tự với tgBHI ta có \(HK\perp BI\)
\(\Rightarrow\widehat{SKH}\) là góc giữa (SBI) và (ABCD)
Xét tg vuông BHI có
\(HK=\dfrac{BI}{2}=\dfrac{a\sqrt{10}}{2}\) (trung tuyến thuộc cạnh huyền)
\(SH\perp\left(ABCD\right);HK\in\left(ABCD\right)\Rightarrow SH\perp HK\)
Xét tg vuông SKH có
\(\tan\widehat{SKH}=\dfrac{SH}{HK}=\dfrac{2a\sqrt{2}}{\dfrac{a\sqrt{10}}{2}}=\dfrac{4\sqrt{5}}{5}\)
còn câu d tôi bận làm sau nhé
Cosx= cos pi/8 là giải phương trình như nào vậy mọi người