Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nghiệm của đa thức M(x) là \(\dfrac{1}{2}\)
\(\Rightarrow x=\dfrac{1}{2}\) để đa thức M(x) = 0
Thay \(x=\dfrac{1}{2}\), ta có:
\(a.\left(\dfrac{1}{2}\right)^2+5.\dfrac{1}{2}-3=0\\ \Rightarrow\dfrac{1}{4}a+\dfrac{5}{2}=3\\ \Rightarrow\dfrac{1}{4}a=3-\dfrac{5}{2}\\ \Rightarrow\dfrac{1}{4}a=\dfrac{1}{2}\\ \Rightarrow a=\dfrac{1}{2}:\dfrac{1}{4}=2\)
Vậy a = 2. Đa thức M(x) được viết đầy đủ dưới dạng:
\(M\left(x\right)=2x^2+5x-3\)
M(x) có nghiệm là 1/2 nên khi x = 1/2 thì M(x) = 0
\(a\left(\dfrac{1}{2}\right)^2+5.\dfrac{1}{2}-3=0\)
\(\Rightarrow a=2\)
Vậy...

Bài 1:
ta có M(x)=a.x2+5.x-3 và x=\(\frac{1}{2}\)
Cho M=0
\(\Rightarrow\)a.1/22+5.1/2-3=0
a.1/4+5/2-3=0
a.1/4-1/2=0
a.1/4=1/2
a=1/2:1/4
a=2
Bài 2
Q(x)=x4+3.x2+1
=x2.x2+1,5.x2+1,5.x2+1,5.1,5-1,25
=x2.(x2+1,5)+1,5.(x2+1,5)-1,25
=(x2+1,5)(x2+1,5)-1,25
\(\Rightarrow\)(x2+1,5)2 \(\ge\)0 với \(\forall\)x
\(\Rightarrow\)(x2+1,5)2-1,25\(\ge\)1,25 > 0
Vậy đa thức Q ko có nghiệm

Bài 1:
1.
$6x^3-2x^2=0$
$2x^2(3x-1)=0$
$\Rightarrow 2x^2=0$ hoặc $3x-1=0$
$\Rightarrow x=0$ hoặc $x=\frac{1}{3}$
Đây chính là 2 nghiệm của đa thức
2.
$|3x+7|\geq 0$
$|2x^2-2|\geq 0$
Để tổng 2 số bằng $0$ thì: $|3x+7|=|2x^2-2|=0$
$\Rightarrow x=\frac{-7}{3}$ và $x=\pm 1$ (vô lý)
Vậy đa thức vô nghiệm.
Bài 2:
1. $x^2+2x+4=(x^2+2x+1)+3=(x+1)^2+3$
Do $(x+1)^2\geq 0$ với mọi $x$ nên $x^2+2x+4=(x+1)^2+3\geq 3>0$ với mọi $x$
$\Rightarrow x^2+2x+4\neq 0$ với mọi $x$
Do đó đa thức vô nghiệm
2.
$3x^2-x+5=2x^2+(x^2-x+\frac{1}{4})+\frac{19}{4}$
$=2x^2+(x-\frac{1}{2})^2+\frac{19}{4}\geq 0+0+\frac{19}{4}>0$ với mọi $x$
Vậy đa thức khác 0 với mọi $x$
Do đó đa thức không có nghiệm.

Vì đa thức \(M_{\left(x\right)}=ax^2+5-3\) có nghiệm là \(\frac{1}{2}\) nên:
\(M\left(\frac{1}{2}\right)=0\Leftrightarrow a\left(\frac{1}{2}\right)^2+5-3=0\)
\(\Rightarrow a.\frac{1}{4}+2=0\)
\(\Rightarrow a.\frac{1}{4}=-2\)
\(\Rightarrow a=-2\div\frac{1}{4}\)
\(\Rightarrow a=-8\)


ta có : \(P\left(\dfrac{-3}{2}\right)=0\)
\(\Leftrightarrow\left(-\dfrac{3}{2}\right)^3-a.\left(-\dfrac{3}{2}\right)^2-2\cdot\dfrac{-3}{2}+4=0\)
\(\Leftrightarrow-\dfrac{27}{8}-\dfrac{9}{4}a+3+4=0\)
\(\Leftrightarrow\cdot\dfrac{9}{4}a=-\dfrac{27}{8}-3-4=-16\)
\(=>a=-16:\dfrac{9}{4}=-\dfrac{64}{9}\)

THAY X=A/2 VÀO ĐA THỨC TA CÓ
M(X)=a*1/4+5*1/2-3=0
vậy a=2

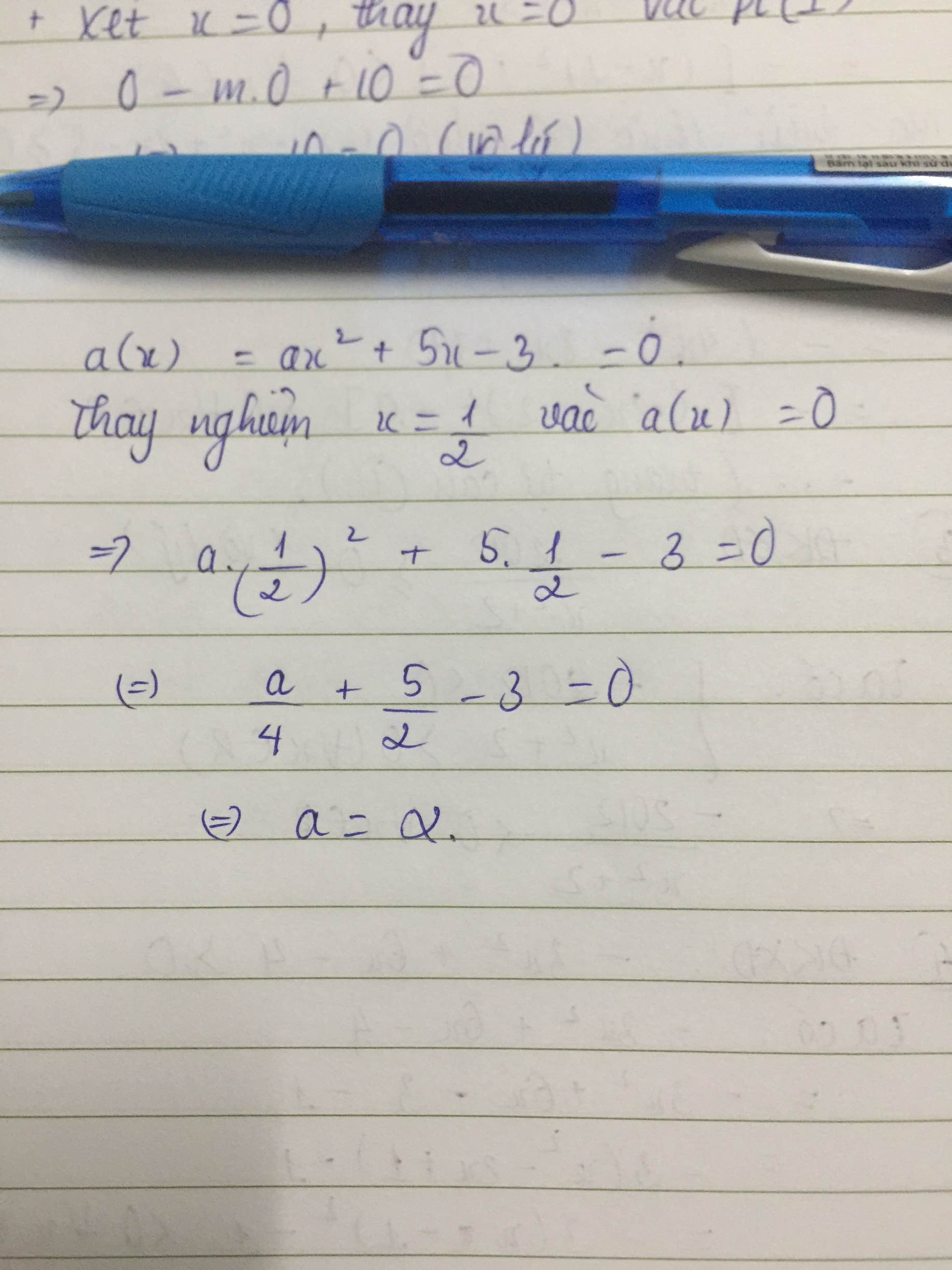
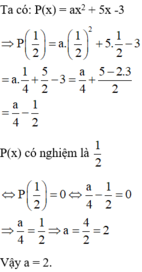
a/ \(M\left(x\right)=-x^2+5\)
Có \(-x^2\le0\forall x\)
=> \(M\left(x\right)\le5\forall x\)
=> M(x) không có nghiệm.
2/
Thay \(x=\dfrac{1}{2}\) vào đa thức M(x) có
\(M\left(\dfrac{1}{2}\right)=\dfrac{1}{4}a+\dfrac{5}{2}-3=0\)
\(\Leftrightarrow\dfrac{1}{4}a=\dfrac{1}{2}\)
\(\Leftrightarrow a=2\)
Vậy...