Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Từ M M ' → + M B → = M A → và áp dụng quy tắc hình bình hành

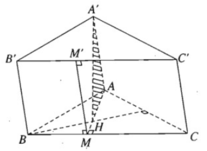
a) BC ⊥ AH và BC ⊥ A'H vì A'H ⊥ (ABC)
⇒ BC ⊥ (A'HA) ⇒ BC ⊥ AA'
Và B'C' ⊥ AA' vì BC // B'C'
b) Ta có AA' // BB' // CC' mà BC ⊥ AA' nên tứ giác BCC’B’ là hình chữ nhật. Vì AA' // (BCC'B') nên ta suy ra MM' ⊥ BC và MM' ⊥ B'C' hay MM’ là đường cao của hình chữ nhật BCC’B’.

Tham khảo
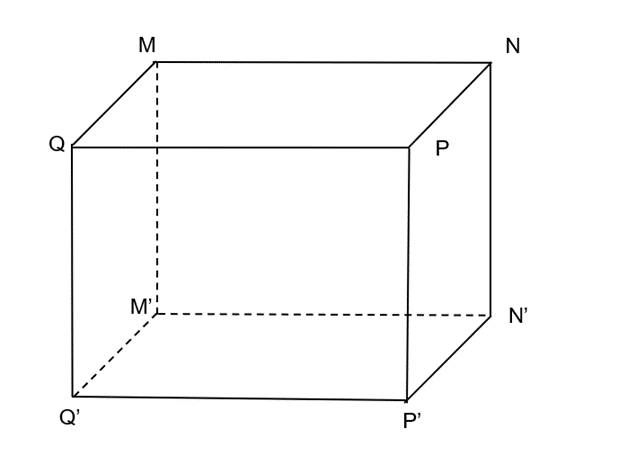
Ta có:
Có NP ⊥ NN'
M'N' ⊥ NN'
=> d(NP, M'N') = NN' = 4a
=>C

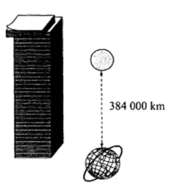
a) giá trị của un rất lớn khi n tăng lên vô hạn
b) Cần n > 384.1010 tờ giấy để đạt được những chồng giấy có về dày lớn hơn khoảng cách từ Trái Đất tới Mặt Trăng

tham khảo:
Đường thẳng vuông góc với mặt phẳng khi đường thẳng đó vuông góc với mọi đường thẳng thuộc mặt phẳng

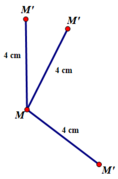
Quy tắc đặt tương ứng điểm M với điểm M’ nêu trên không phải là một phép biến hình vì M’không phải là điểm duy nhất được xác định trên mặt phẳng
Ví dụ minh họa: a = 4 cm

Gọi d' là đường thẳng qua M và vuông góc d
\(\Rightarrow\) d' nhận (2;1) là 1 vtpt
Phương trình d':
\(2\left(x-1\right)+1\left(y-0\right)=0\Leftrightarrow2x+y-2=0\)
Gọi A là giao điểm của d và d' \(\Rightarrow\) tọa độ A là nghiệm:
\(\left\{{}\begin{matrix}x-2y=0\\2x+y-2=0\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{4}{5};\dfrac{2}{5}\right)\)
Gọi M' là điểm đối xứng M qua d \(\Rightarrow A\) là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_A-x_M=\dfrac{3}{5}\\y_{M'}=2y_A-y_M=\dfrac{4}{5}\end{matrix}\right.\)
Vậy \(M'\left(\dfrac{3}{5};\dfrac{4}{5}\right)\)