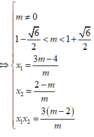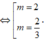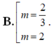bạn đùa à? @@

\(2^4-4^2=16-16=0\)

biết làm rồi

có 3 đường tiệm cận là: x\(=\pm4\)

y\(=0\)

a: \(=3\cdot25-16:4=75-4=71\)

b: =20-30+1=-10+1=-9

c: \(=2^3\cdot3=24\)

Đặt \(t=2^x\left(t>0\right)\) thì phương trình trở thành 

\(4t^2-2t.4-\left(t^4+2t^3\right)=0\)

Bây giờ coi 4=u là một ẩn của phương trình, còn t là số đã biết. Phương trình trở thành phương trình bậc 2 đối với ẩn u. Tính \(\Delta'\)

ta có :

\(\Delta'=\left(-t\right)^2+\left(t^4+2t^3\right)=\left(t^2+t\right)^2\)

Do đó :

\(\begin{cases}u=t-t\left(t+1\right)\\u=t+t\left(t+1\right)\end{cases}\) \(\Leftrightarrow\begin{cases}4=-t^2\\4=t^2+2t\end{cases}\) \(\Leftrightarrow t^2+2t-4=0\)

                             \(\Leftrightarrow\begin{cases}t=-1-\sqrt{5}\\t=-1+\sqrt{5}\end{cases}\)

Suy ra \(2^x=\sqrt{5}-1\Leftrightarrow x=\log_2\left(\sqrt{5}+1\right)\)

1.

PT $\Leftrightarrow 2^{x^2-5x+6}+2^{1-x^2}-2^{7-5x}-1=0$

$\Leftrightarrow (2^{x^2-5x+6}-2^{7-5x})-(1-2^{1-x^2})=0$

$\Leftrightarrow 2^{7-5x}(2^{x^2-1}-1)-(2^{x^2-1}-1)2^{1-x^2}=0$

$\Leftrightarrow (2^{x^2-1}-1)(2^{7-5x}-2^{1-x^2})=0$

$\Rightarrow 2^{x^2-1}-1=0$ hoặc $2^{7-5x}-2^{1-x^2}=0$

Nếu $2^{x^2-1}=1\Leftrightarrow x^2-1=0$

$\Leftrightarrow x^2=1\Leftrightarrow x=\pm 1$

$2^{7-5x}-2^{1-x^2}=0$

$\Leftrightarrow 7-5x=1-x^2\Leftrightarrow x^2-5x+6=0$

$\Leftrightarrow (x-2)(x-3)=0\Leftrightarrow x=2; x=3$

2. Đặt $\sin ^2x=a$ thì $\cos ^2x=1-a$. PT trở thành:

$16^a+16^{1-a}=10$

$\Leftrightarrow 16^a+\frac{16}{16^a}=10$

$\Leftrightarrow (16^a)^2-10.16^a+16=0$

Đặt $16^a=x$ thì:

$x^2-10x+16=0$

$\Leftrightarrow (x-2)(x-8)=0$

$\Leftrightarrow x=2$ hoặc $x=8$

$\Leftrightarrow 16^a=2$ hoặc $16^a=8$

$\Leftrightarrow 2^{4a}=2$ hoặc $2^{4a}=2^3$

$\Leftrightarroww 4a=1$ hoặc $4a=3$

$\Leftrightarrow a=\frac{1}{4}$ hoặc $a=\frac{3}{4}$

Nếu $a=\frac{1}{4}\Leftrightarrow \sin ^2x=\frac{1}{4}$

$\Leftrightarrow \sin x=\pm \frac{1}{2}$

Nếu $a=\sin ^2x=\frac{3}{4}\Rightarrow \sin x=\pm \frac{\sqrt{3}}{2}$

Đến đây thì đơn giản rồi.

\(A=\left(3\sqrt{3}\right)^{\frac{4}{3}}+\left(\frac{1}{16}\right)^{\frac{3}{4}}+2\left(\frac{8}{27}\right)^{\frac{2}{3}}\)

\(A=\left(3\sqrt{3}\right)^{\frac{4}{3}}+55+\frac{32}{3}\)

\(A=\left(3\sqrt{3}\right)^{\frac{4}{3}}+\frac{197}{3}\)

\(A=243+\frac{197}{3}\)

\(A=\frac{926}{3}\)

Ta có \(A=3^{\frac{3}{2}.\frac{4}{3}}+\left(\frac{1}{2}\right)^{4.\frac{3}{4}}+2\left(\frac{2}{3}\right)^{3.\frac{2}{3}}=3^2+\left(\frac{1}{2}\right)^3+2\left(\frac{2}{3}\right)^2=\frac{721}{72}\)

Chọn D.

Đường thẳng d đi qua M(11;0;-25) và có vectơ chỉ phương 

Gọi H là hình chiếu của I trên (d). Ta có:

Chọn B

y ' = m x 2 - 2 ( m - 1 ) x + 3 ( m - 2 )

Yêu cầu của bài toán ⇔ y ' = 0  có hai nghiệm phân biệt x 1 , x 2  thỏa mãn: x 1 + 2 x 2 = 1