Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
Gọi \(M\left(x;y;z\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(1-x;2-y;-3-z\right)\\\overrightarrow{MB}=\left(-2-x;-y;2-z\right)\end{matrix}\right.\)
\(2\overrightarrow{MA}=\overrightarrow{MB}\Rightarrow\left\{{}\begin{matrix}2-2x=-2-x\\4-2y=-y\\-6-2z=2-z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=4\\y=4\\z=-8\end{matrix}\right.\) \(\Rightarrow M\left(4;4;-8\right)\)
2.
Ta có:
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-2;2;-4\right)\\\overrightarrow{AC}=\left(0;1;c-2\right)\end{matrix}\right.\)
Tam giác ABC vuông tại A \(\Rightarrow AB\perp AC\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=0\)
\(\Rightarrow-2.0+2.1-4\left(c-2\right)=0\)
\(\Rightarrow c=\dfrac{5}{2}\)
Vậy \(C\left(1;0;\dfrac{5}{2}\right)\)

Chọn B
Quãng đường vật di chuyển sau thời gian 4 giây bằng :
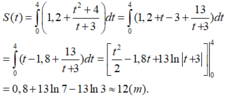

Ta có \(y'=-3<0\) nên hàm số luôn nghịch biến với mọi $x$ thuộc tập xác định.
Do đó kết hợp với \(x<2\) nên \(y>y(2)=-4\)
Dấu bằng không xảy ra cho nên hàm không có min.

1) Ta có \(y'=\left(x^6\left(1-x\right)^5\right)'\)
\(=\left(x^6\right)'\left(1-x\right)^5+\left[\left(1-x\right)^5\right]'.x^6\)
\(=6x^5\left(1-x\right)^5+5\left(1-x\right)^4\left(1-x\right)'.x^6\)
\(=6x^5\left(1-x\right)^5-5x^6\left(1-x\right)^4\)
\(=x^5\left(1-x\right)^4\left[6\left(1-x\right)-5x\right]\)
\(=x^5\left(1-x\right)^4\left(6-11x\right)\)
\(y'=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=\dfrac{6}{11}\end{matrix}\right.\)
Vậy hàm số đã cho đạt cực trị tại \(x=0,x=1,x=\dfrac{11}{6}\)
2) Có \(y'=-2.\left(2x\right)'\sin2x\) \(=-4\sin2x\)
\(y'=0\Leftrightarrow\sin2x=0\) \(\Leftrightarrow2x=k\pi\left(k\inℤ\right)\) \(\Leftrightarrow x=\dfrac{k\pi}{2}\) \(\left(k\inℤ\right)\)
Vậy hàm số đã cho đạt cực trị tại \(x=\dfrac{k\pi}{2}\left(k\inℤ\right)\)

Do \(f\left(x\right)\) nghịch biến \(\Rightarrow\min\limits_{\left[1;2\right]}f\left(x\right)=f\left(2\right)\); \(\max\limits_{\left[1;2\right]}=f\left(1\right)\)
Thay \(x=1\) vào ta được:
\(f^2\left(1\right)-f\left(1\right)=6\Rightarrow f^2\left(1\right)-f\left(1\right)-6=0\Rightarrow\left[{}\begin{matrix}f\left(1\right)=3\\f\left(1\right)=-2\end{matrix}\right.\)
Thay \(x=2\) vào ta được:
\(f^2\left(2\right)-2f\left(2\right)-120=0\Rightarrow\left[{}\begin{matrix}f\left(2\right)=12>f\left(1\right)\left(l\right)\\f\left(2\right)=-10\end{matrix}\right.\)
\(\Rightarrow\min\limits_{\left[1;2\right]}f\left(x\right)=-10\)
Đạo hàm 2 vế giả thiết:
\(\left[f'\left(x\right)-1\right]f\left(x\right)+f'\left(x\right)\left[f\left(x\right)-x\right]=6x^5+12x^3+4x\)
- Nếu \(f\left(1\right)=3\) thay \(x=1\) vào biểu thức trên ta được:
\(\left[f'\left(1\right)-1\right].3+f'\left(1\right).\left[3-1\right]=22\) \(\Rightarrow f'\left(1\right)=5>0\) (vô lý do \(f\left(x\right)\) nghịch biến trên R nên \(f'\left(x\right)< 0\) \(\forall x\))
\(\Rightarrow f\left(1\right)=-2\Rightarrow\max\limits_{\left[1;2\right]}f\left(x\right)=-2\)

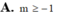
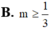
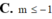
Kết quả : =?...